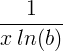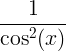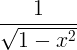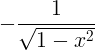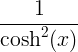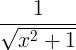Izvedena pravila

Izvedena pravila i zakoni. Tabela derivata funkcija.

Definicija izvedenice
Izvedena pravila
Tabela derivata funkcija
Izvedeni primjeri

Definicija izvedenice

Izvod funkcije je omjer razlike vrijednosti funkcije f (x) u točkama x + Δx i x s Δx, kada je Δx beskonačno malen. Izvod je nagib funkcije ili nagib tangente u točki x.

$f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}$

Druga izvedenica

Drugi izvod dan je:

Ili jednostavno izvedite prvu izvedenicu:

N-ti derivat

N th derivat izračunava izvođenja f (x) n puta.

A n th izvedeni jednaka derivat (n-1) derivat:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

Primjer:

Pronađi četvrtu izvedenicu od

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] '' '' = [10 x ⁴ ] '' = = [40 x ³ ] '' = [120 x ² ] '= 240 x

Izvedena na grafu funkcije

Izvod funkcije je nagib tangencijalne crte.

Izvedena pravila

Pravilo izvedenice izvoda	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Pravilo izvedenog proizvoda	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Izvedeno količničko pravilo	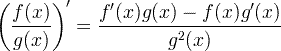$\ lijevo (\ frac {f (x)} {g (x)} \ desno) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}$
Pravilo izvedenog lanca	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Pravilo izvedenice izvoda

Kada su a i b konstante.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Primjer:

Pronađi izvedenicu od:

3 x ² + 4 x.

Prema pravilu zbroja:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Pravilo izvedenog proizvoda

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Izvedeno količničko pravilo

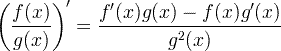
$\ lijevo (\ frac {f (x)} {g (x)} \ desno) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}$

Pravilo izvedenog lanca

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Ovo se pravilo može bolje razumjeti Lagrangeovim zapisom:

$\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}$

Funkcionalna aproksimacija

Za male Δx možemo dobiti aproksimaciju f (x ₀ + Δx), kada znamo f (x ₀ ) i f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Tabela derivata funkcija

Naziv funkcije	Funkcija	Izvedena
Naziv funkcije	f ( x )	f '( x )
Konstantno	konst	0
Linearno	x	1
Vlast	x ^a	sjekira ^a-¹
Eksponencijalno	e ^x	e ^x
Eksponencijalno	a ^x	a ^x ln a
Prirodni logaritam	ln ( x )
Logaritam	zapisnik _b ( x )
Sinus	grijeh x	cos x
Kosinus	cos x	-grijeh x
Tangens	preplanuli x
Arcsine	arcsin x
Arccosine	arccos x
Arktangens	arktan x
Hiperbolički sinus	sinh x	cosh x
Hiperbolički kosinus	cosh x	sinh x
Hiperbolička tangenta	tanh x
Inverzni hiperbolički sinus	sinh ^-1 x
Inverzni hiperbolički kosinus	cosh ^-1 x
Inverzna hiperbolična tangenta	tanh ^-1 x