Varijansa

U vjerojatnosti i statistici, varijansa slučajne varijable je prosječna vrijednost kvadratne udaljenosti od srednje vrijednosti. Predstavlja način na koji je slučajna varijabla raspoređena u blizini srednje vrijednosti. Mala varijanca ukazuje na to da je slučajna varijabla raspoređena u blizini srednje vrijednosti. Velika varijanca ukazuje na to da je slučajna varijabla distribuirana daleko od srednje vrijednosti. Na primjer, uz normalnu raspodjelu, uska krivulja zvona imat će malu varijancu, a široka krivulja zvona veliku varijancu.

Definicija varijance

Varijansa slučajne varijable X je očekivana vrijednost kvadrata razlike X i očekivana vrijednost μ.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

Iz definicije varijance možemo dobiti

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Varijansa kontinuirane slučajne varijable

Za kontinuiranu slučajnu varijablu sa srednjom vrijednošću μ i funkcijom gustoće vjerojatnosti f (x):

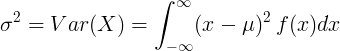
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

ili

Var (X) = \ lijevo [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ desno] - \ mu ^ 2

Varijansa diskretne slučajne varijable

Za diskretnu slučajnu varijablu X sa srednjom vrijednošću μ i funkcijom mase vjerojatnosti P (x):

\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

ili

Var (X) = \ lijevo [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ desno] - \ mu ^ 2

Svojstva varijance

Kada su X i Y neovisne slučajne varijable:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

Standardno odstupanje ►

 

Vidi također

VJEROJATNOST I STATISTIKA
BRZE TABLICE