Raspodjela vjerojatnosti
U vjerojatnosti i statistici distribucija je karakteristika slučajne varijable, opisuje vjerojatnost slučajne varijable u svakoj vrijednosti.
Svaka raspodjela ima određenu funkciju gustoće vjerojatnosti i funkciju raspodjele vjerojatnosti.
Iako postoji neograničen broj raspodjele vjerojatnosti, koristi se nekoliko uobičajenih raspodjela.
Funkcija kumulativne raspodjele
Raspodjela vjerojatnosti opisana je kumulativnom funkcijom raspodjele F (x),
što je vjerojatnost slučajne varijable X da dobije vrijednost manju ili jednaku x:
F ( x ) = P ( X ≤ x )
Kontinuirana distribucija
Kumulativna funkcija raspodjele F (x) izračunava se integracijom funkcije gustoće vjerojatnosti f (u) kontinuirane slučajne varijable X.
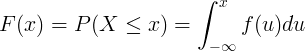
Diskretna raspodjela
Kumulativna funkcija raspodjele F (x) izračunava se zbrajanjem funkcije vjerojatnosti mase P (u) diskretne slučajne varijable X.
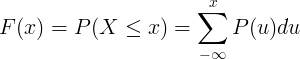
Tablica kontinuiranih distribucija
Kontinuirana raspodjela je raspodjela kontinuirane slučajne varijable.
Primjer kontinuirane distribucije
...
Tablica kontinuiranih distribucija
| Naziv distribucije | Simbol distribucije | Funkcija gustoće vjerojatnosti (pdf) | Podlo | Varijansa |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Uobičajeno / gaussian | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Uniformu | X ~ U ( a , b ) |
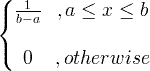 |
|
|
| Eksponencijalno | X ~ exp (λ) | |
|
|
| Gama | X ~ gama ( c , λ) | 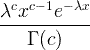 x / 0, c / 0, λ/ 0 |
|
|
| Chi kvadrat | X ~ χ 2 ( k ) |
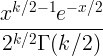 |
k |
2 k |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Beta | ||||
| Weibull | ||||
| Log-normalno | X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Regrutovati | ||||
| Riža | ||||
| Studentska t |
Tablica diskretnih raspodjela
Diskretna raspodjela je raspodjela diskretne slučajne varijable.
Primjer diskretne raspodjele
...
Tablica diskretnih raspodjela
| Naziv distribucije | Simbol distribucije | Funkcija mase vjerojatnosti (pmf) | Podlo | Varijansa | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Binomni | X ~ spremnik ( n , p ) |
|
np |
np (1- str ) |
|
| Poisson | X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Uniformu | X ~ U ( a, b ) |
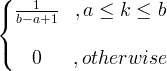 |
|
|
|
| Geometrijski | X ~ Geom ( p ) |
|
|
|
|
| Hiper-geometrijska | X ~ HG ( N , K , n ) |
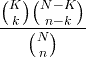 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernoulli | X ~ Bern ( p ) |
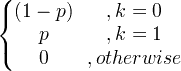 |
p |
p (1- p ) |
|
Vidi također
VJEROJATNOST I STATISTIKA
- Osnovna vjerojatnost
- Očekivanje
- Varijansa
- Standardno odstupanje
- Raspodjela vjerojatnosti
- Normalna distribucija
- Statistički simboli
BRZE TABLICE