Funkcija Arccos (x)
Arccos (x), cos -1 (x), inverzna kosinusna funkcija.
Definicija arccosa
Arkkosinus x definiran je kao inverzna kosinusna funkcija x kada je -1≤x≤1.
Kada je kosinus y jednak x:
cos y = x
Tada je arkkosinus x jednak inverznoj kosinusnoj funkciji x, koja je jednaka y:
arccos x = cos -1 x = y
(Ovdje cos -1 x znači inverzni kosinus i ne znači kosinus snage -1).
Primjer
arccos 1 = cos -1 1 = 0 rad = 0 °
Grafikon arkosa
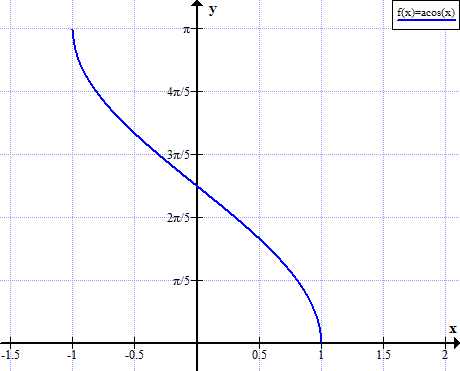
Arccos vlada
| Naziv pravila | Pravilo |
|---|---|
| Kosinus arkozina | cos (arccos x ) = x |
| Arckosinus kosinusa | arccos (cos x ) = x + 2 k π, kada je k ∈ℤ ( k je cijeli broj) |
| Arccos negativnog argumenta | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Komplementarni kutovi | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Arccos zbroj | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Razlika u arccosima | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos grijeha x | arccos (sin x ) = - x - (2 k +0,5) π |
| Sinus arccosine-a | |
| Tangenta arkozina |  |
| Derivat arkozina | 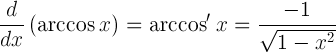 |
| Neodređeni integral arkozina | |
Stol Arccos
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Vidi također
- Funkcija kosinusa
- Funkcija Arcsine
- Funkcija arktana
- Arccos kalkulator
- Pretvarač radijana u stupnjeve
- Arccos od 0
- Arccos od 1
- Arccos od 2
- Arccos od 3
- Arccos od cos
- Arccos grijeha
- Derivat arccosa
- Graf arccosa
- Cos arccosa
- Grijeh arccosa
- Preplanuli ten arccosa