Perbedaan

Dalam probabilitas dan statistik, varians variabel acak adalah nilai rata-rata jarak kuadrat dari nilai rata-rata. Ini mewakili bagaimana variabel acak didistribusikan mendekati nilai rata-rata. Varians kecil menunjukkan bahwa variabel acak didistribusikan mendekati nilai rata-rata. Varians besar menunjukkan bahwa variabel acak didistribusikan jauh dari nilai rata-rata. Sebagai contoh, pada distribusi normal, kurva lonceng sempit akan memiliki varians kecil dan kurva lonceng lebar memiliki varian yang besar.

Definisi varians

Varians variabel acak X adalah nilai yang diharapkan dari kuadrat selisih X dan nilai yang diharapkan μ.

σ ² = Var ( X ) = E [( X - μ ) ² ]

Dari definisi varians yang bisa kita dapatkan

σ ² = Var ( X ) = E ( X ² ) - μ ²

Varians variabel acak kontinu

Untuk variabel acak kontinu dengan nilai rata-rata μ dan fungsi kepadatan probabilitas f (x):

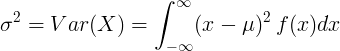
$\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx$

atau

$Var (X) = \ kiri [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2$

Varians variabel acak diskrit

Untuk variabel acak diskrit X dengan nilai rata-rata μ dan fungsi massa probabilitas P (x):

$\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)$

atau

$Var (X) = \ kiri [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ kanan] - \ mu ^ 2$

Sifat varians

Ketika X dan Y adalah variabel acak independen:

Var ( X + Y ) = Var ( X ) + Var ( Y )

Deviasi standar ►

Perbedaan

Definisi varians

Varians variabel acak kontinu

Varians variabel acak diskrit

Sifat varians

Var ( X + Y ) = Var ( X ) + Var ( Y )

Lihat juga

PROBABILITAS & STATISTIK

TABEL CEPAT