Standar Deviasi

Dalam probabilitas dan statistik, deviasi standar variabel acak adalah jarak rata-rata variabel acak dari nilai rata-rata.

Ini mewakili bagaimana variabel acak didistribusikan mendekati nilai rata-rata. Standar deviasi kecil menunjukkan bahwa variabel acak didistribusikan mendekati nilai rata-rata. Standar deviasi yang besar menunjukkan bahwa variabel acak didistribusikan jauh dari nilai rata-rata.

Rumus definisi deviasi standar

Simpangan baku adalah akar kuadrat dari varians variabel acak X, dengan nilai rata-rata μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Dari definisi deviasi standar bisa kita dapatkan

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Simpangan baku variabel acak kontinu

Untuk variabel acak kontinu dengan nilai rata-rata μ dan fungsi kepadatan probabilitas f (x):

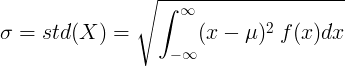
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

atau

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Simpangan baku dari variabel acak diskrit

Untuk variabel acak diskrit X dengan nilai rata-rata μ dan fungsi massa probabilitas P (x):

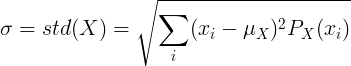
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

atau

\ sigma = std (X) = \ sqrt {\ kiri [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ kanan] - \ mu ^ 2}

 

Distribusi probabilitas ►

 

Lihat juga

PROBABILITAS & STATISTIK
TABEL CEPAT