Distribusi kemungkinan

Dalam distribusi probabilitas dan statistik merupakan karakteristik dari variabel acak, menggambarkan probabilitas variabel acak pada setiap nilai.

Setiap distribusi memiliki fungsi kepadatan probabilitas dan fungsi distribusi probabilitas tertentu.

Meskipun ada jumlah distribusi probabilitas yang tidak pasti, ada beberapa distribusi umum yang digunakan.

Distribusi probabilitas dijelaskan oleh fungsi distribusi kumulatif F (x),

yang merupakan probabilitas variabel acak X untuk mendapatkan nilai yang lebih kecil dari atau sama dengan x:

F ( x ) = P ( X ≤ x )

Fungsi distribusi kumulatif F (x) dihitung dengan integrasi fungsi kepadatan probabilitas f (u) dari variabel acak kontinu X.

Fungsi distribusi kumulatif F (x) dihitung dengan penjumlahan fungsi massa probabilitas P (u) dari variabel acak diskrit X.

Distribusi kontinu adalah distribusi variabel acak kontinu.

...

Nama distribusi	Simbol distribusi	Fungsi kepadatan probabilitas (pdf)	Berarti	Perbedaan
		f _X ( x )	μ = E ( X )	σ ² = Var ( X )
Normal / gaussian	X ~ N (μ, σ ² )	$\ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}}$	μ	σ ²
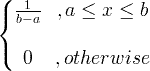Seragam	X ~ U ( a , b )	$\ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, jika tidak \ end {matrix}$		$\ frac {(ba) ^ 2} {12}$
Eksponensial	X ~ exp (λ)	$\ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix}$	$\ frac {1} {\ lambda}$	$\ frac {1} {\ lambda ^ 2}$
Gamma	X ~ gamma ( c , λ)	$\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}$ x / 0, c / 0, λ/ 0	$\ frac {c} {\ lambda}$	$\ frac {c} {\ lambda ^ 2}$
Chi square	X ~ χ ² ( k )	$\ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}$	k	2 k
Wishart
F	X ~ F ( k ₁, k ₂ )
Beta
Weibull
Log-normal	X ~ LN (μ, σ ² )
Rayleigh
Cauchy
Dirichlet
Laplace
Retribusi
Nasi
Mahasiswa t

Distribusi diskrit adalah distribusi variabel acak diskrit.

...

Nama distribusi	Simbol distribusi	Fungsi massa probabilitas (pmf)		Berarti	Perbedaan
		f _x ( k ) = P ( X = k ) k = 0,1,2, ...		E ( x )	Var ( x )
Binomium	X ~ Bin ( n , p )	$\ binom {n} {k} p ^ {k} (1-p) ^ {nk}$		np	np (1- p )
Poisson	X ~ Poisson (λ)		λ ≥ 0	λ	λ
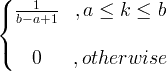Seragam	X ~ U ( a, b )	$\ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, jika tidak \ end {matrix}$		$\ frac {a + b} {2}$	$\ frac {(b-a + 1) ^ {2} -1} {12}$
Geometris	X ~ Geom ( p )	$p (1-p) ^ {k}$		$\ frac {1-p} {p}$	$\ frac {1-p} {p ^ 2}$
Hiper-geometris	X ~ HG ( N , K , n )		N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N	$\ frac {nK} {N}$	$\ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}$
Bernoulli	X ~ Bern ( p )	$\ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, jika tidak \ end {matrix}$		p	p (1- p )

Lihat juga