Rumus Probabilitas Dasar

 

Rentang Probabilitas

0 ≤ P ( A ) ≤ 1

Aturan Acara Pelengkap

P ( A C ) + P ( A ) = 1

Aturan Penambahan

P (A∪B) = P (A) + P (B) - P (A∩B)

Peristiwa Terpisah

Acara A dan B terputus-putus jikaf

P (A∩B) = 0

Probabilitas Bersyarat

P (A | B) = P (A∩B) / P (B)

Formula Bayes

P (A | B) = P (B | A) ⋅ P (A) / P (B)

Acara Independen

Peristiwa A dan B bersifat independen iff

P (A∩B) = P (A) ⋅ P (B)

Fungsi Distribusi Kumulatif

F X ( x ) = P ( X ≤ x )

Fungsi Massa Probabilitas

jumlah (i = 1..n, P (X = x (i)) = 1

Fungsi Kepadatan Probabilitas

fX (x) = dFX (x) / dx

FX (x) = integral (-inf..x, fX (y) * dy)

FX (x) = jumlah (k = 1..x, P (X = k))

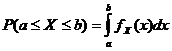
P (a <= X <= b) = integral (a..b, fX (x) * dx)

integral (-inf..inf, fX (x) * dx) = 1

 

Kovarian

Cox (X, Y) = E (X-uy) (Y-uy) = E (XY) - ux * uy

Korelasi

corr (X, Y) = Cov (X, Y) / (Std (X) * Std (Y))

 

Bernoulli: 0-gagal 1-sukses

Geometris: 0-gagal 1-berhasil

Hipergeometri: N objek dengan K objek sukses, n objek diambil.

 

 

 
 
PROBABILITAS & STATISTIK
TABEL CEPAT