Funzione arcoseno
arcsin (x), sin -1 (x), funzione seno inversa .
Definizione di Arcsin
L'arcoseno di x è definito come la funzione seno inversa di x quando -1≤x≤1.
Quando il seno di y è uguale a x:
sin y = x
Allora l'arcoseno di x è uguale alla funzione seno inversa di x, che è uguale a y:
arcsin x = sin -1 x = y
Esempio
arcsin 1 = sin -1 1 = π / 2 rad = 90 °
Grafico di arcsin
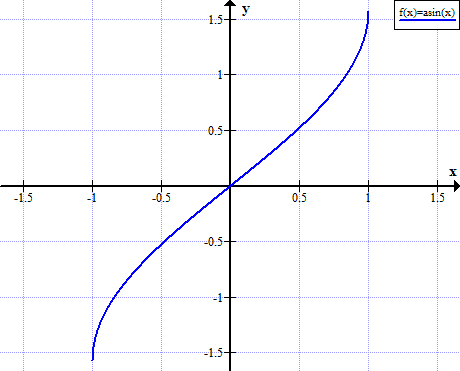
Regole di Arcsin
| Nome regola | Regola |
|---|---|
| Seno di arcoseno | sin (arcsin x ) = x |
| Arcoseno del seno | arcsin (sin x ) = x +2 k π, quando k ∈ℤ ( k è intero) |
| Arcsin di argomento negativo | arcsin (- x ) = - arcsin x |
| Angoli complementari | archi x = π / 2 - archi x = 90 ° - archi x |
| Somma di arcsin | arcsin α + arcsin ( β ) = arcsin ( α√ (1- β 2 ) + β√ (1- α 2 ) ) |
| Differenza di arcsin | arcsin α - arcsin ( β ) = arcsin ( α√ (1- β 2 ) - β√ (1- α 2 ) ) |
| Coseno di arcoseno | |
| Tangente dell'arcoseno | |
| Derivato dell'arcoseno | 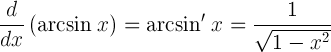 |
| Integrale indefinito di arcoseno |
Tavolo Arcsin
| x | arcsin (x) (rad) |
arcsin (x) (°) |
|---|---|---|
| -1 | -π / 2 | -90 ° |
| -√ 3 /2 | -π / 3 | -60 ° |
| -√ 2 /2 | -π / 4 | -45 ° |
| -1/2 | -π / 6 | -30 ° |
| 0 | 0 | 0 ° |
| 1/2 | π / 6 | 30 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 3 | 60 ° |
| 1 | π / 2 | 90 ° |
Guarda anche
- Funzione seno
- Funzione arcoseno
- Funzione Arctan
- Calcolatrice Arcsin
- Convertitore da gradi a radianti
- Arcsin di 0
- Arcsin di 1
- Arcsin of infinity
- Grafico di Arcsin
- Derivato di arcsin
- Integrale di Arcsin
- Peccato di arcsin
- Cos di arcsin
- Tan di arcsin