積分
統合は、派生の逆の操作です。
関数の積分は、関数のグラフの下の領域です。
不定積分の定義
いつ
![]()
不定積分特性
![]()
![]()
![]()
![]()
![]()
![]()
積分変数の変更
いつ
![]() そして
そして
![]()
![]()
部品による統合
![]()
積分表
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
定積分の定義
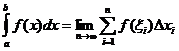
いつ
![]()
![]()
![]()
定積分計算
いつ
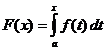 、
、
![]()
![]() そして
そして
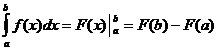
明確な積分特性
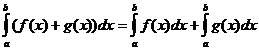
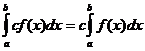
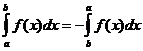
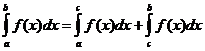
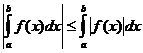
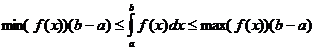 いつ
いつ
![]()
積分変数の変更
いつ
![]() 、
、
![]() 、
、
![]() 、
、
![]()
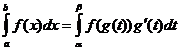
部品による統合
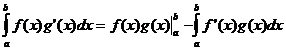
平均値の定理
場合F(xは)連続している点があります
![]() そう
そう
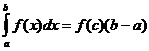
定積分の台形近似
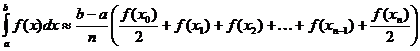
ガンマ関数
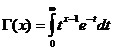
ガンマ関数は、x/ 0で収束します。
ガンマ関数のプロパティ
G (x +1)= x G (x )
G (n +1)= n !、 場合N ℕ (正の整数)。
![]()
ベータ関数
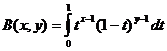
ベータ関数とガンマ関数の関係