Arccos(x)関数
Arccos(x)、cos -1(x)、逆余弦関数。
Arccosの定義
xのアークコサインは、-1≤x≤1の場合のxの逆コサイン関数として定義されます。
yのコサインがxに等しい場合:
cos y = x
次に、xのアークコサインはxの逆コサイン関数に等しく、これはyに等しくなります。
arccos x = cos -1 x = y
(ここで、cos -1 xは逆余弦を意味し、-1の累乗の余弦を意味するものではありません)。
例
arccos 1 = cos -1 1 = 0 rad = 0°
arccosのグラフ
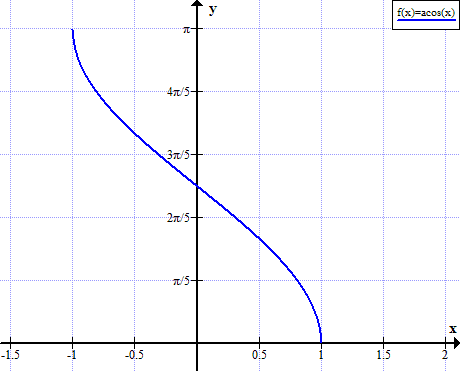
Arccosのルール
| ルール名 | ルール |
|---|---|
| アークコサインのコサイン | cos(arccos x)= x |
| コサインのアークコサイン | ARCCOS(COS X)= X + 2 k個のπ、Kの∈ℤ(kは整数) |
| 否定的な議論のArccos | ARCCOS( - X)=π - ARCCOS X = 180° - ARCCOS X |
| 補角 | ARCCOS X =π/ 2 -アークサインX = 90° -アークサインX |
| Arccosの合計 | ARCCOS(α)+ ARCCOS(β)= ARCCOS(αβ - √ (1- α 2)(1- β 2)) |
| Arccosの違い | ARCCOS(α) - ARCCOS(β)= ARCCOS(αβ + √ (1- α 2)(1- β 2)) |
| xの罪のアークコス | ARCCOS(罪X)= - X - (2 K +0.5)π |
| アークコサインの正弦 | |
| アークコサインのタンジェント |  |
| アルコシンの誘導体 | 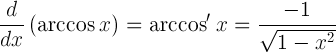 |
| アークコサインの不定積分 | |
Arccosテーブル
| x | arccos(x) (rad) |
arccos(x) (°) |
|---|---|---|
| -1 | π | 180° |
| -√ 3 /2 | 5π/ 6 | 150° |
| -√2 / 2 / | 3π/ 4 | 135° |
| -1/2 | 2π/ 3 | 120° |
| 0 | π/ 2 | 90° |
| 1/2 | π/ 3 | 60° |
| √2 / 2 / | π/ 4 | 45° |
| √ 3 /2 | π/ 6 | 30° |
| 1 | 0 | 0° |
も参照してください
- 余弦関数
- アークサイン関数
- Arctanfunction
- Arccos計算機
- ラジアンから度へのコンバーター
- 0のArccos
- 1のArccos
- 2のArccos
- 3のArccos
- cosのArccos
- 罪のアークコス
- Arccos派生物
- Arccosグラフ
- arccosのCos
- arccosの罪
- アルコスの日焼け