Integral

La integración es la operación inversa de la derivación.

La integral de una función es el área debajo de la gráfica de la función.

Definición integral indefinida

Cuando dF (x) / dx = f (x) =/ integral (f (x) * dx) = F (x) + c

Propiedades integrales indefinidas

integral (f (x) + g (x)) * dx = integral (f (x) * dx) + integral (g (x) * dx)

integral (a * f (x) * dx) = a * integral (f (x) * dx)

integral (f (a * x) * dx) = 1 / a * F (a * x) + c

integral (f (x + b) * dx) = F (x + b) + c

integral (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

integral (df (x) / dx * dx) = f (x)

Variable de cambio de integración

Cuando x = g (t)  y dx = g '(t) * dt

integral (f (x) * dx) = integral (f (g (t)) * g '(t) * dt)

Integración por partes

integral (f (x) * g '(x) * dx) = f (x) * g (x) - integral (f' (x) * g (x) * dx)

Tabla de integrales

integral (f (x) * dx = F (x) + c

integral (a * dx) = a * x + c

integral (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, cuando a </ - 1

integral (1 / x * dx) = ln (abs (x)) + c

integral (e ^ x * dx) = e ^ x + c

integral (a ^ x * dx) = a ^ x / ln (x) + c

integral (ln (x) * dx) = x * ln (x) - x + c

integral (sin (x) * dx) = -cos (x) + c

integral (cos (x) * dx) = sin (x) + c

integral (tan (x) * dx) = -ln (abs (cos (x))) + c

integral (arcosen (x) * dx) = x * arcosen (x) + sqrt (1-x ^ 2) + c

integral (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

integral (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

integral (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

integral (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

integral (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

integral (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

integral (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

integral (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

integral (senh (x) * dx) = cosh (x) + c

integral (cosh (x) * dx) = sinh (x) + c

integral (tanh (x) * dx) = ln (cosh (x)) + c

 

Definición integral definida

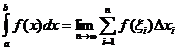
integral (a..b, f (x) * dx) = lim (n-/ inf, sum (i = 1..n, f (z (i)) * dx (i)))  

Cuando x0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Cálculo integral definido

Cuando  ,

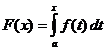  dF (x) / dx = f (x)  y

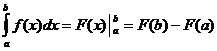
integral (a..b, f (x) * dx) = F (b) - F (a)  

Propiedades integrales definidas

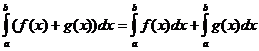
integral (a..b, (f (x) + g (x)) * dx) = integral (a..b, f (x) * dx) + integral (a..b, g (x) * dx )

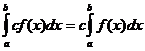
integral (a..b, c * f (x) * dx) = c * integral (a..b, f (x) * dx)

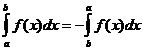
integral (a..b, f (x) * dx) = - integral (b..a, f (x) * dx)

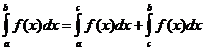
integral (a..b, f (x) * dx) = integral (a..c, f (x) * dx) + integral (c..b, f (x) * dx)

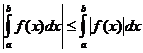
abs (integral (a..b, f (x) * dx)) <= integral (a..b, abs (f (x)) * dx)

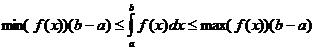min (f (x)) * (ba) <= integral (a..b, f (x) * dx) <= max (f (x)) * (ba)  cuando x miembro de [a, b]

Variable de cambio de integración

Cuando x = g (t)  , dx = g '(t) * dt  , g (alfa) = a  , g (beta) = b

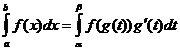
integral (a..b, f (x) * dx) = integral (alfa..beta, f (g (t)) * g '(t) * dt)

Integración por partes

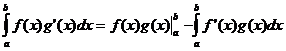
integral (a..b, f (x) * g '(x) * dx) = integral (a..b, f (x) * g (x) * dx) - integral (a..b, f' (x) * g (x) * dx)

Teorema del valor medio

Cuando f ( x ) es continua hay un punto c es miembro de [a, b]  entonces

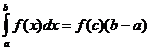
integral (a..b, f (x) * dx) = f (c) * (ba)   

Aproximación trapezoidal de la integral definida

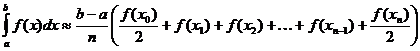
integral (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

La función gamma

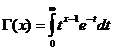
gamma (x) = integral (0..inf, t ^ (x-1) * e ^ (- t) * dt

La función Gamma es convergente para x/ 0 .

Propiedades de la función gamma

G ( x +1) = x G ( x )

G ( n +1) = n ! , cuando n ℕ (entero positivo). es miembro de

La función beta

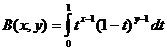
B (x, y) = integral (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Relación función beta y función gamma

B (x, y) = Gamma (x) * Gamma (y) / Gamma (x + y)

 

 

 

CÁLCULO
MESAS RÁPIDAS