e സ്ഥിരാങ്കം
e സ്ഥിരാങ്കം അല്ലെങ്കിൽ യൂളറിന്റെ നമ്പർ ഒരു ഗണിതശാസ്ത്ര സ്ഥിരാങ്കമാണ്. ഇ സ്ഥിരാങ്കം യഥാർത്ഥവും യുക്തിരഹിതവുമായ സംഖ്യയാണ്.
e = 2.718281828459 ...
ഇ യുടെ നിർവചനം
ഇ സ്ഥിരാങ്കത്തെ പരിധിയായി നിർവചിച്ചിരിക്കുന്നു:
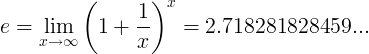
ഇതര നിർവചനങ്ങൾ
ഇ സ്ഥിരാങ്കത്തെ പരിധിയായി നിർവചിച്ചിരിക്കുന്നു:
![]()
ഇ സ്ഥിരാങ്കത്തെ അനന്തമായ ശ്രേണിയായി നിർവചിച്ചിരിക്കുന്നു:
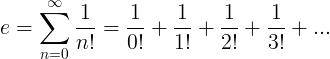
ഇ
ഇ
E യുടെ പരസ്പരവിരുദ്ധമായ പരിധി:
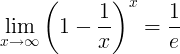
ഇ യുടെ ഡെറിവേറ്റീവുകൾ
എക്സ്പോണൻഷ്യൽ ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവ് എക്സ്പോണൻഷ്യൽ ഫംഗ്ഷനാണ്:
( e x ) '= e x
സ്വാഭാവിക ലോഗരിതം ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവ് പരസ്പര പ്രവർത്തനമാണ്:
(ലോഗ് ഇ x ) '= (ln x )' = 1 / x
ഇ
എക്സ്പൊണൻഷ്യൽ ഫംഗ്ഷൻ അനിശ്ചിതകാല അവിഭാജ്യ ഇ X എക്സ്പൊണൻഷ്യൽ ഫംഗ്ഷൻ ഇ X .
∫ ഇ X DX = ഇ എക്സ് + C
സ്വാഭാവിക ലോഗരിതം ഫംഗ്ഷന്റെ അനിശ്ചിതകാല അവിഭാജ്യ ലോഗ് ഇ X ആണ്:
∫ ലോഗ് e x dx = ∫ ln x dx = x ln x - x + c
1 / x എന്ന പരസ്പരപ്രവർത്തനത്തിന്റെ 1 മുതൽ e വരെയുള്ള നിർദ്ദിഷ്ട ഇന്റഗ്രൽ 1:
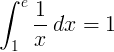
അടിസ്ഥാന ഇ ലോഗരിതം
X എന്ന സംഖ്യയുടെ സ്വാഭാവിക ലോഗരിതം x ന്റെ അടിസ്ഥാന ഇ ലോഗരിതം ആയി നിർവചിക്കപ്പെടുന്നു:
ln x = ലോഗ് ഇ x
എക്സ്പോണൻഷ്യൽ പ്രവർത്തനം
എക്സ്പോണൻഷ്യൽ ഫംഗ്ഷൻ നിർവചിച്ചിരിക്കുന്നത്:
f ( x ) = exp ( x ) = e x
യൂളറിന്റെ സൂത്രവാക്യം
സങ്കീർണ്ണ സംഖ്യയായ e iθ ന് ഐഡന്റിറ്റി ഉണ്ട്:
ഇ ഇθ = കോസ് ( θ ) + ഞാൻ പാപം ( θ )
i എന്നത് സാങ്കൽപ്പിക യൂണിറ്റാണ് (-1 ന്റെ വർഗ്ഗമൂലം).
Real ഏതെങ്കിലും യഥാർത്ഥ സംഖ്യയാണ്.
ഇതും കാണുക
- 2.71828183 എങ്ങനെയാണ്?
- ലോഗരിതം നിയമങ്ങൾ
- സ്വാഭാവിക ലോഗരിതം
- എക്സ്പോണന്റ്സ് നിയമങ്ങൾ
- സാധാരണ വിതരണം
- പൈ സ്ഥിരാങ്കം
- e സ്ഥിരാങ്കം - വിക്കിപീഡിയ