എക്‌സ്‌പോണന്റ് നിയമങ്ങൾ

എക്‌സ്‌പോണന്റ് നിയമങ്ങൾ, എക്‌സ്‌പോണന്റ് നിയമങ്ങൾ, ഉദാഹരണങ്ങൾ.

എന്താണ് ഒരു എക്‌സ്‌പോണന്റ്

N ന്റെ ശക്തിയിലേക്ക് ഉയർത്തിയ അടിസ്ഥാനം a, n തവണയുടെ ഗുണനത്തിന് തുല്യമാണ്:

a n = a × a × ... × a

                    n തവണ

a അടിസ്ഥാനവും n എക്‌സ്‌പോണന്റുമാണ്.

ഉദാഹരണങ്ങൾ

3 1 = 3

3 2 = 3 × 3 = 9

3 3 = 3 × 3 × 3 = 27

3 4 = 3 × 3 × 3 × 3 = 81

3 5 = 3 × 3 × 3 × 3 × 3 = 243

എക്‌സ്‌പോണന്റുകളുടെ നിയമങ്ങളും ഗുണങ്ങളും

റൂളിന്റെ പേര് ഭരണം ഉദാഹരണം
ഉൽപ്പന്ന നിയമങ്ങൾ ഒരു n ⋅ ഒരു മീറ്റർ = ഒരു n + M 2 3 ⋅ 2 4 = 2 3 + 4 = 128
ഒരു n ⋅ ബി n = ( ഒരു ⋅ ബി ) n 3 2 ⋅ 4 2 = (3⋅4) 2 = 144
ഉചിതമായ നിയമങ്ങൾ a n / a m = a n - m 2 5 /2 3 = 2 ൫-൩ = 4
a n / b n = ( a / b ) n 4 3 /2 3 = (൪/൨) 3 = 8
പവർ നിയമങ്ങൾ ( b n ) m = b n⋅m (2 3 ) 2 = 2 3⋅2 = 64
b n m = b ( n m ) 2 3 2 = 2 ( 3 2 ) = 512
m √ ( b n ) = b n / m 2 (2 6 ) = 2 6/2 = 8
b 1 / n = n √ b 8 1/3 = 3 √ 8 = 2
നെഗറ്റീവ് എക്‌സ്‌പോണന്റുകൾ b -n = 1 / b n 2 -3 = 1/2 3 = 0.125
പൂജ്യം നിയമങ്ങൾ b 0 = 1 5 0 = 1
0 n = 0, n / 0 ന് 0 5 = 0
ഒരു നിയമങ്ങൾ b 1 = ബി 5 1 = 5
1 n = 1 1 5 = 1
മൈനസ് വൺ റൂൾ 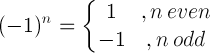(-1) 5 = -1
ഡെറിവേറ്റീവ് റൂൾ ( x n ) ' = n ⋅ x n -1 ( x 3 ) ' = 3⋅ x 3-1
ഇന്റഗ്രൽ റൂൾ ∫ X n DX = X n +1 ചെയ്യുക / ( n +1 ചെയ്യുക), സി ∫ X 2 DX = X 2 +1 / (2 +1) + സി

എക്‌സ്‌പോണന്റുകൾ ഉൽപ്പന്ന നിയമങ്ങൾ

ഒരേ അടിത്തറയുള്ള ഉൽപ്പന്ന നിയമം

ഒരു n ⋅ ഒരു മീറ്റർ = ഒരു n + M

ഉദാഹരണം:

2 3 2 4 = 2 3 + 4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128

ഒരേ എക്‌സ്‌പോണന്റുള്ള ഉൽപ്പന്ന നിയമം

ഒരു n ⋅ ബി n = ( ഒരു ⋅ ബി ) n

ഉദാഹരണം:

3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 12⋅12 = 144

കാണുക: എക്‌സ്‌പോണന്റുകൾ ഗുണിക്കുന്നു

എക്‌സ്‌പോണന്റുകൾ ഘടക നിയമങ്ങൾ

ഒരേ അടിത്തറയുള്ള ക്വാണ്ടന്റ് റൂൾ

a n / a m = a n - m

ഉദാഹരണം:

2 5 /2 3 = 2 ൫-൩ = 2 2 = 2⋅2 = 4

ഒരേ എക്‌സ്‌പോണന്റുള്ള ക്വാണ്ടന്റ് റൂൾ

a n / b n = ( a / b ) n

ഉദാഹരണം:

4 3 /2 3 = (൪/൨) 3 = 2 3 = 2⋅2⋅2 = 8

കാണുക: എക്‌സ്‌പോണന്റുകളെ വിഭജിക്കുന്നു

എക്‌സ്‌പോണന്റുകൾ പവർ റൂളുകൾ

പവർ റൂൾ I.

( a n ) m = a n⋅m

ഉദാഹരണം:

(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64

പവർ റൂൾ II

a n m = a ( n m )

ഉദാഹരണം:

2 3 2 = 2 (3 2 ) = 2 (3⋅3) = 2 9 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512

റാഡിക്കലുകളുള്ള പവർ റൂൾ

m √ ( a n ) = a n / m

ഉദാഹരണം:

2 (2 6 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8

നെഗറ്റീവ് എക്‌സ്‌പോണന്റുകൾ ഭരണം നടത്തുന്നു

b -n = 1 / b n

ഉദാഹരണം:

2 -3 = 1/2 3 = 1 / (2⋅2⋅2) = 1/8 = 0.125

കാണുക: നെഗറ്റീവ് എക്‌സ്‌പോണന്റുകൾ

 

എക്‌സ്‌പോണന്റ് കാൽക്കുലേറ്റർ

 

ഇതും കാണുക

NUMBERS
ദ്രുത പട്ടികകൾ