Arccos (x) -funksjon
Arccos (x), cos -1 (x), invers cosinusfunksjon .
Arccos definisjon
Arccosine av x er definert som den inverse cosinusfunksjonen til x når -1≤x≤1.
Når cosinus av y er lik x:
cos y = x
Da er arkkosinen til x lik den omvendte cosinusfunksjonen til x, som er lik y:
arccos x = cos -1 x = y
(Her betyr cos -1 x det inverse cosinus og betyr ikke cosinus til kraften -1).
Eksempel
arccos 1 = cos -1 1 = 0 rad = 0 °
Graf av arccos
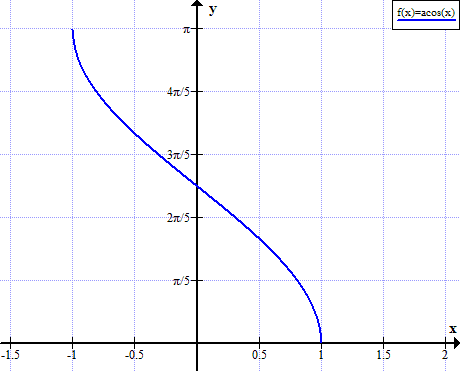
Arccos regler
| Regelnavn | Regel |
|---|---|
| Kosinus av arkkosin | cos (arccos x ) = x |
| Arccosine of cosinus | arccos (cos x ) = x + 2 k π, når k ∈ℤ ( k er heltall) |
| Arccos av negativt argument | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Utfyllende vinkler | arccos x = π / 2 - bueform x = 90 ° - bueform x |
| Arccos sum | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Arccos forskjell | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos of sin of x | arccos (sin x ) = - x - (2 k +0,5) π |
| Sinke av arkkosin | |
| Tangent av arkkosin | 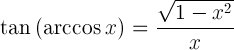 |
| Derivat av arkkosin | 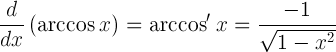 |
| Ubestemt integral av arkkosin | |
Arccos bord
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3- / 2- | 5π / 6 | 150 ° |
| -√ 2- / 2- | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2- / 2- | π / 4 | 45 ° |
| √ 3- / 2- | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Se også
- Kosinusfunksjon
- Arcsine funksjon
- Arktanfunksjon
- Arccos kalkulator
- Radianer til grader omformer
- Arccos på 0
- Arccos på 1
- Arccos av 2
- Arccos på 3
- Arccos of cos
- Syndebuer
- Arccos-derivat
- Arccos-graf
- Cos av arccos
- Synd av arccos
- Brun av arccos