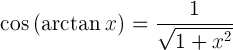Funkcja Arcus tangens

Arctan (x), tan ^-1 (x), odwrotna funkcja styczna .

• Definicja arctan
• Wykres arctanu
• Zasady Arktanu
• Stół Arctan
• Kalkulator arktański

Definicja Arktanu

Arcus tangens x jest definiowany jako odwrotna funkcja styczna x, gdy x jest rzeczywiste (x ∈ℝ ).

Gdy styczna y jest równa x:

tan y = x

Wtedy arcus tangens x jest równy odwrotnej funkcji stycznej x, która jest równa y:

arctan x = tan ^-1 x = y

Przykład

arctan 1 = tan ^-1 1 = π / 4 rad = 45 °

Wykres arctanu

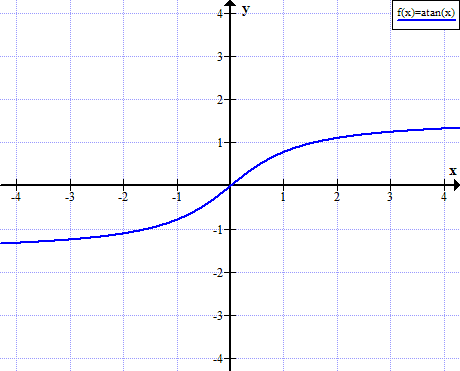
Zasady Arktanu

Nazwa reguły	Reguła
Styczna arcus tangensa	tan (arctan x ) = x
Arktan argumentu negatywnego	arctan (- x ) = - arctan x
Suma arktańska	arctan α + arctan β = arctan [( α + β ) / (1- αβ )]
Różnica arktańska	arctan α - arctan β = arctan [( α - β ) / (1+ αβ )]
Sinus arcus tangensa
Cosinus arcus tangensa
Wzajemna argumentacja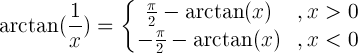
Arctan z arcsin
Pochodna arctanu
Całka nieoznaczona arctanu

Stół Arctan

x	arctan (x) (rad)	arctan (x) (°)
-∞	-π / 2	-90 °
-3	-1,2490	-71,565 °
-2	-1,1071	-63,435 °
-√ 3	-π / 3	-60 °
-1	-π / 4	-45 °
-1 / √ 3	-π / 6	-30 °
-0,5	-0,4636	-26,565 °
0	0	0 °
0.5	0,4636	26,565 °
1 / √ 3	π / 6	30 °
1	π / 4	45 °
√ 3	π / 3	60 °
2	1.1071	63,435 °
3	1.2490	71,565 °
∞	π / 2	90 °

 

 

---

Zobacz też

• Funkcja styczna
• Funkcja Arccosine
• Funkcja Arcsine
• Arktan z 0
• Arktan z 1
• Arktan z 2
• Arktan nieskończoności
• Pochodna arctanu
• Całka z arctanu
• Sinus arctan
• Cosinus arktanu
• Wykres Arktan
• Kalkulator arktański
• Konwerter stopni na radiany