Número Zero (0)
- Definição de número zero
- Histórico de número zero
- Propriedades de número zero
- Conjuntos que contêm zero
Definição de número zero
Zero é um número usado em matemática para descrever nenhuma quantidade ou quantidade nula.
Quando há 2 maçãs na mesa e pegamos as 2 maçãs, podemos dizer que não há maçãs na mesa.
O número zero não é um número positivo e nem um número negativo.
O zero também é um dígito de espaço reservado em outros números (por exemplo: 40,103, 170).
Zero é um número?
Zero é um número. Não é um número positivo nem negativo.
Dígito zero
O dígito zero é usado como um espaço reservado ao escrever números.
Por exemplo:
204 = 2 × 100 + 0 × 10 + 4 × 1
Histórico de número zero
Quem inventou o número zero?
O moderno símbolo 0 foi inventado na Índia no século 6, usado mais tarde pelos persas e árabes e mais tarde na Europa.
Símbolo de zero
O número zero é denotado com o símbolo 0 .
O sistema de numeração árabe usa o símbolo ٠.
Propriedades de número zero
x representa qualquer número.
| Operação | Regra | Exemplo |
|---|---|---|
Adição |
x + 0 = x |
3 + 0 = 3 |
Subtração |
x - 0 = x |
3 - 0 = 3 |
Multiplicação |
x × 0 = 0 |
5 × 0 = 0 |
Divisão |
0 ÷ x = 0 , quando x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 é indefinido |
5 ÷ 0 é indefinido |
|
Exponenciação |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Raiz |
√ 0 = 0 |
|
Logaritmo |
log b (0) é indefinido |
|
| |
||
Fatorial |
0! = 1 |
|
Seno |
sen 0º = 0 |
|
Cosine |
cos 0º = 1 |
|
Tangente |
tan 0º = 0 |
|
Derivado |
0 '= 0 |
|
Integrante |
∫ 0 d x = 0 + C |
|
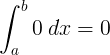 |
Adição zero
A adição de um número mais zero é igual ao número:
x + 0 = x
Por exemplo:
5 + 0 = 5
Subtração zero
A subtração de um número menos zero é igual ao número:
x - 0 = x
Por exemplo:
5 - 0 = 5
Multiplicação por zero
A multiplicação de um número vezes zero é igual a zero:
x × 0 = 0
Por exemplo:
5 × 0 = 0
Número dividido por zero
A divisão de um número por zero não está definida:
x ÷ 0 é indefinido
Por exemplo:
5 ÷ 0 é indefinido
Zero dividido por um número
A divisão de um zero por um número é zero:
0 ÷ x = 0
Por exemplo:
0 ÷ 5 = 0
Número à potência zero
A potência de um número elevado a zero é um:
x 0 = 1
Por exemplo:
5 0 = 1
Logaritmo de zero
O logaritmo de base b de zero é indefinido:
log b (0) é indefinido
Não há número com o qual possamos aumentar a base b para chegar a zero.
Apenas o limite do logaritmo de base b de x, quando x converge para zero é menos infinito:
![]()
Conjuntos que contêm zero
Zero é um elemento dos conjuntos de números naturais, números inteiros, números reais e complexos:
| Definir | Definir notação de associação |
|---|---|
| Números naturais (não negativos) | 0 ∈ ℕ 0 |
| Números inteiros | 0 ∈ ℤ |
| Numeros reais | 0 ∈ ℝ |
| Números complexos | 0 ∈ ℂ |
| Números racionais | 0 ∈ ℚ |
O zero é um número par ou ímpar?
O conjunto de números pares é:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
O conjunto de números ímpares é:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Zero é um múltiplo inteiro de 2:
0 × 2 = 0
Zero é um membro do conjunto de números pares:
0 ∈ {2 k , k ∈ℤ}
Portanto, zero é um número par e não um número ímpar.
O zero é um número natural?
Existem duas definições para o conjunto de números naturais.
O conjunto de inteiros não negativos:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
O conjunto de inteiros positivos:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Zero é um membro do conjunto de inteiros não negativos:
0 ∈ ℕ 0
Zero não é membro do conjunto de inteiros positivos:
0 ∉ ℕ 1
O zero é um número inteiro?
Existem três definições para os números inteiros:
O conjunto de números inteiros:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
O conjunto de inteiros não negativos:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
O conjunto de inteiros positivos:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Zero é um membro do conjunto de números inteiros e do conjunto de inteiros não negativos:
0 ∈ ℤ
0 ∈ ℕ 0
Zero não é membro do conjunto de inteiros positivos:
0 ∉ ℕ 1
O zero é um número inteiro?
O conjunto de números inteiros:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Zero é um membro do conjunto de números inteiros:
0 ∈ ℤ
Portanto, zero é um número inteiro.
O zero é um número racional?
Um número racional é um número que pode ser expresso como o quociente de dois números inteiros:
ℚ = { n / m ; n , m ∈ℤ}
Zero pode ser escrito como um quociente de dois números inteiros.
Por exemplo:
0 = 0/3
Portanto, zero é um número racional.
O zero é um número positivo?
Um número positivo é definido como um número maior que zero:
x / 0
Por exemplo:
5/ 0
Visto que zero não é maior que zero, não é um número positivo.
O zero é um número primo?
O número 0 não é um número primo.
Zero não é um número positivo e possui um número infinito de divisores.
O menor número primo é 2.