интеграл

Интеграция - это операция, обратная деривации.

Интеграл функции - это площадь под графиком функции.

Неопределенное интегральное определение

когда dF (x) / dx = f (x) =/ интеграл (f (x) * dx) = F (x) + c

Неопределенные интегральные свойства

интеграл (f (x) + g (x)) * dx = интеграл (f (x) * dx) + интеграл (g (x) * dx)

интеграл (a * f (x) * dx) = a * интеграл (f (x) * dx)

интеграл (f (a * x) * dx) = 1 / a * F (a * x) + c

интеграл (f (x + b) * dx) = F (x + b) + c

интеграл (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

интеграл (df (x) / dx * dx) = f (x)

Изменение переменной интеграции

когда х = г (т)  а также dx = g '(t) * dt

интеграл (f (x) * dx) = интеграл (f (g (t)) * g '(t) * dt)

Интеграция по частям

интеграл (f (x) * g '(x) * dx) = f (x) * g (x) - интеграл (f' (x) * g (x) * dx)

Таблица интегралов

интеграл (f (x) * dx = F (x) + c

интеграл (a * dx) = a * x + c

интеграл (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, когда a </ - 1

интеграл (1 / x * dx) = ln (abs (x)) + c

интеграл (e ^ x * dx) = e ^ x + c

интеграл (a ^ x * dx) = a ^ x / ln (x) + c

интеграл (ln (x) * dx) = x * ln (x) - x + c

интеграл (sin (x) * dx) = -cos (x) + c

интеграл (cos (x) * dx) = sin (x) + c

интеграл (tan (x) * dx) = -ln (abs (cos (x))) + c

интеграл (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

интеграл (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

интеграл (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

интеграл (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

интеграл (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

интеграл (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

интеграл (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

интеграл (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

интеграл (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

интеграл (sinh (x) * dx) = ch (x) + c

интеграл (ch (x) * dx) = sinh (x) + c

интеграл (tanh (x) * dx) = ln (ch (x)) + c

 

Определенное интегральное определение

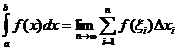
интеграл (a..b, f (x) * dx) = lim (n-/ inf, sum (i = 1..n, f (z (i)) * dx (i)))  

когда х0 = а, хп = Ь

dx (k) = x (k) - x (k-1)

х (к-1) <= z (k) <= x (k)

Расчет определенного интеграла

когда  ,

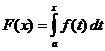  dF (х) / dx = f (х)  а также

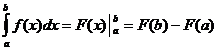
интеграл (a..b, f (x) * dx) = F (b) - F (a)  

Определенные интегральные свойства

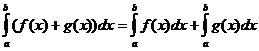
интеграл (a..b, (f (x) + g (x)) * dx) = интеграл (a..b, f (x) * dx) + интеграл (a..b, g (x) * dx )

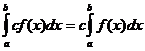
интеграл (a..b, c * f (x) * dx) = c * интеграл (a..b, f (x) * dx)

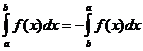
интеграл (a..b, f (x) * dx) = - интеграл (b..a, f (x) * dx)

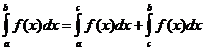
интеграл (a..b, f (x) * dx) = интеграл (a..c, f (x) * dx) + интеграл (c..b, f (x) * dx)

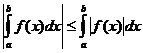
абс (интеграл (a..b, f (x) * dx)) <= интеграл (a..b, abs (f (x)) * dx)

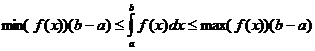min (f (x)) * (ba) <= интеграл (a..b, f (x) * dx) <= max (f (x)) * (ba)  когда x член [a, b]

Изменение переменной интеграции

когда х = г (т)  , dx = g '(t) * dt  , г (альфа) = а  , g (бета) = b

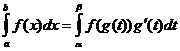
интеграл (a..b, f (x) * dx) = интеграл (alpha..beta, f (g (t)) * g '(t) * dt)

Интеграция по частям

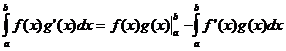
интеграл (a..b, f (x) * g '(x) * dx) = интеграл (a..b, f (x) * g (x) * dx) - интеграл (a..b, f' (х) * g (x) * dx)

Теорема о среднем значении

Когда f ( x ) непрерывна, существует точка c является членом [a, b]  так

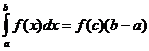
интеграл (a..b, f (x) * dx) = f (c) * (ba)   

Трапецеидальная аппроксимация определенного интеграла

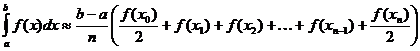
интеграл (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

Гамма-функция

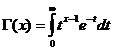
гамма (x) = интеграл (0..inf, t ^ (x-1) * e ^ (- t) * dt

Гамма-функция сходится при x/ 0 .

Свойства гамма-функции

G ( х +1) = х G ( х )

G ( п +1) = п ! , когда n ℕ (положительное целое число). является членом

Бета-функция

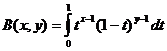
B (x, y) = интеграл (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Связь бета-функции и гамма-функции

B (x, y) = гамма (x) * гамма (y) / гамма (x + y)

 

 

 

ИСЧИСЛЕНИЕ
БЫСТРЫЕ ТАБЛИЦЫ