e konštantná
Konštanta alebo Eulerovo číslo je matematická konštanta. Konštanta e je skutočné a iracionálne číslo.
e = 2,718281828459 ...
Definícia e
Konštanta e je definovaná ako hranica:
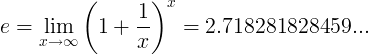
Alternatívne definície
Konštanta e je definovaná ako hranica:
![]()
Konstanta e je definovaná ako nekonečná séria:
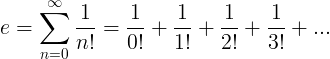
Vlastnosti napr
Recipročný napr
Prevrátená hodnota e je limit:
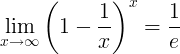
Deriváty napr
Derivátom exponenciálnej funkcie je exponenciálna funkcia:
( e x ) '= e x
Derivátom prirodzenej logaritmickej funkcie je recipročná funkcia:
(log e x ) '= (ln x )' = 1 / x
Integrály e
Neurčitý integrál exponenciálnej funkcie e x je exponenciálna funkcia e x .
∫ e x dx = e x + c
Neurčitý integrál prirodzeného logaritmického funkčného protokolu e x je:
∫ log e x dx = ∫ ln x dx = x ln x - x + c
Definitívny integrál od 1 do e recipročnej funkcie 1 / x je 1:
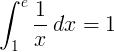
Základný e logaritmus
Prirodzený logaritmus čísla x je definovaný ako základný logaritmus čísla x:
ln x = prihlásiť e x
Exponenciálna funkcia
Exponenciálna funkcia je definovaná ako:
f ( x ) = exp ( x ) = e x
Eulerov vzorec
Komplexné číslo e iθ má identitu:
e iθ = cos ( θ ) + i sin ( θ )
i je imaginárna jednotka (druhá odmocnina z -1).
θ je akékoľvek reálne číslo.
Pozri tiež
- Ako je to 2,71828183?
- Pravidlá logaritmu
- Prirodzený logaritmus
- Pravidlá exponentov
- Normálne rozdelenie
- Pi konštantná
- e konštanta - wikipedia