Nulové číslo (0)
- Definícia nulového čísla
- História nulových čísel
- Vlastnosti nulového čísla
- Sady, ktoré obsahujú nulu
Definícia nulového čísla
Nula je číslo používané v matematike na opísanie nulovej alebo nulovej veličiny.
Keď sú na stole 2 jablká a vezmeme 2 jablká, môžeme povedať, že na stole je nula jabĺk.
Nulové číslo nie je kladné a záporné číslo.
Nula je tiež zástupná číslica v iných číslach (napr. 40 103, 170).
Je nula číslo?
Nula je číslo. Nie je to kladné ani záporné číslo.
Nulová číslica
Pri písaní čísel sa ako zástupný symbol používa nulová číslica.
Napríklad:
204 = 2 × 100 + 0 × 10 + 4 × 1
História nulových čísel
Kto vymyslel nulové číslo?
Moderný symbol 0 bol vynájdený v Indii v 6. storočí, používaný neskôr Peržanmi a Arabmi a neskôr v Európe.
Symbol nuly
Nulové číslo je označené symbolom 0 .
Arabská číselná sústava používa symbol ٠.
Vlastnosti nulového čísla
x predstavuje ľubovoľné číslo.
| Prevádzka | Pravidlo | Príklad |
|---|---|---|
Dodatok |
x + 0 = x |
3 + 0 = 3 |
Odčítanie |
x - 0 = x |
3 - 0 = 3 |
Násobenie |
x × 0 = 0 |
5 × 0 = 0 |
Divízia |
0 ÷ x = 0 , keď x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 nie je definované |
5 ÷ 0 nie je definované |
|
Umocnenie |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Koreň |
√ 0 = 0 |
|
Logaritmus |
log b (0) nie je definovaný |
|
| |
||
Faktoriál |
0! = 1 |
|
Sínus |
hriech 0º = 0 |
|
Kosínus |
cos 0 ° = 1 |
|
Tečna |
tan 0 ° = 0 |
|
Derivát |
0 '= 0 |
|
Integrálne |
∫ 0 d x = 0 + C. |
|
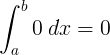 |
Nulový prírastok
Sčítanie čísla plus nula sa rovná číslu:
x + 0 = x
Napríklad:
5 + 0 = 5
Nulové odčítanie
Odčítanie čísla mínus nula sa rovná číslu:
x - 0 = x
Napríklad:
5 - 0 = 5
Násobenie nulou
Násobenie čísla krát nula sa rovná nule:
x × 0 = 0
Napríklad:
5 × 0 = 0
Číslo delené nulou
Delenie čísla nulou nie je definované:
x ÷ 0 nie je definované
Napríklad:
5 ÷ 0 nie je definované
Nula delená číslom
Delenie nuly číslom je nula:
0 ÷ x = 0
Napríklad:
0 ÷ 5 = 0
Číslo do nulového výkonu
Sila čísla zvýšeného o nulu je jedna:
x 0 = 1
Napríklad:
5 0 = 1
Logaritmus nuly
Nulový základný b logaritmus je nedefinovaný:
log b (0) nie je definovaný
Nie je žiadne číslo, s ktorým by sme mohli zdvihnúť základňu b, aby sme dostali nulu.
Iba limit základného b logaritmu x, keď x konverguje nulu, je mínus nekonečno:
![]()
Sady, ktoré obsahujú nulu
Nula je prvkom množiny prirodzených čísel, celých čísel, reálnych čísel a komplexných čísel:
| Nastaviť | Nastaviť členskú notáciu |
|---|---|
| Prirodzené čísla (nezáporné) | 0 ∈ ℕ 0 |
| Celé čísla | 0 ∈ ℤ |
| Reálne čísla | 0 ∈ ℝ |
| Komplexné čísla | 0 ∈ ℂ |
| Racionálne čísla | 0 ∈ ℚ |
Je nula párne alebo nepárne číslo?
Sada párnych čísel je:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Sada nepárnych čísel je:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Nula je celočíselný násobok 2:
0 × 2 = 0
Nula je členom sady párnych čísel:
0 ∈ {2 k , k ∈ℤ}
Takže nula je párne číslo a nie nepárne číslo.
Je nula prirodzené číslo?
Pre prirodzené čísla existujú dve definície.
Sada nezáporných celých čísel:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Sada kladných celých čísel:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Nula je členom množiny nezáporných celých čísel:
0 ∈ ℕ 0
Nula nie je členom množiny kladných celých čísel:
0 ∉ ℕ 1
Je nula celé číslo?
Pre celé čísla existujú tri definície:
Sada celých čísel:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Sada nezáporných celých čísel:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Sada kladných celých čísel:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Nula je členom množiny celých čísel a množiny nezáporných celých čísel:
0 ∈ ℤ
0 ∈ ℕ 0
Nula nie je členom množiny kladných celých čísel:
0 ∉ ℕ 1
Je nula celé číslo?
Sada celých čísel:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Nula je členom množiny celých čísel:
0 ∈ ℤ
Takže nula je celé číslo.
Je nula racionálne číslo?
Racionálne číslo je číslo, ktoré možno vyjadriť ako kvocient dvoch celých čísel:
ℚ = { n / m ; n , m ∈ℤ}
Nulu je možné zapísať ako kvocient dvoch celých čísel.
Napríklad:
0 = 0/3
Takže nula je racionálne číslo.
Je nula kladné číslo?
Kladné číslo je definované ako číslo, ktoré je väčšie ako nula:
x / 0
Napríklad:
5/ 0
Pretože nula nie je väčšia ako nula, nejde o kladné číslo.
Je nula prvočíslo?
Číslo 0 nie je prvočíslo.
Nula nie je kladné číslo a má nekonečný počet deliteľov.
Najnižšie prvočíslo je 2.