Квадратна једначина
Квадратна једначина је полином другог реда са 3 коефицијента - а , б , ц .
Квадратна једначина дата је:
секира 2 + бк + ц = 0
Решење квадратне једначине дато је са 2 броја к 1 и к 2 .
Квадратну једначину можемо променити у облик:
( к - к 1 ) ( к - к 2 ) = 0
Квадратна формула
Решење квадратне једначине даје квадратна формула:
![]()
Израз унутар квадратног корена назива се дискриминантан и означава се са Δ:
Δ = б 2 - 4 ац
Квадратна формула са дискриминантним записом:
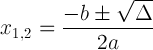
Овај израз је важан јер нам може рећи о решењу:
- Када је Δ/ 0, постоје 2 стварна корена к 1 = (- б + √ Δ ) / (2а) и к 2 = (- б-√ Δ ) / (2а) .
- Када је Δ = 0, постоји један корен к 1 = к 2 = -б / (2а) .
- Када Δ <0, не постоје реални коренови, постоје 2 сложене корени:
к 1 = (- б + и√ -Δ ) / (2а) и к 2 = (- би√ -Δ ) / (2а) .
Проблем # 1
3 к 2 +5 к +2 = 0
решење:
а = 3, б = 5, ц = 2
к 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
к 1 = (-5 + 1) / 6 = -4/6 = -2/3
к 2 = (-5 - 1) / 6 = -6/6 = -1
Проблем # 2
3 к 2 -6 к +3 = 0
решење:
а = 3, б = -6, ц = 3
к 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
к 1 = к 2 = 1
Проблем # 3
к 2 +2 к +5 = 0
решење:
а = 1, б = 2, ц = 5
к 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Правих решења нема. Вредности су сложени бројеви:
к 1 = -1 + 2 и
к 2 = -1 - 2 и
Квадратни граф функције
Квадратна функција је полиномска функција другог реда:
ф ( к ) = ос 2 + бк + ц
Решења квадратне једначине су корени квадратне функције, односно тачке пресека графа квадратне функције са к-осом, када
ф ( к ) = 0
Када постоје 2 пресечне тачке графика са к-осом, постоје 2 решења квадратне једначине.
Када постоји 1 тачка пресека графика са к-осом, постоји 1 решење квадратне једначине.
Када нема пресечних тачака графика са к-осом, не добијамо стварна решења (или 2 сложена решења).