Природни логаритам - лн (к)
Природни логаритам је логаритам базе е броја.
- Дефиниција природног логаритма (лн)
- Правила и својства природног логаритма (лн)
- Сложени логаритам
- Графикон лн (к)
- Табела природних логаритама (лн)
- Калкулатор природног логаритма
Дефиниција природног логаритма
Када
е и = к
Тада је основни е логаритам к
лн ( к ) = лог е ( к ) = и
Е константа или Ојлеров број је:
е ≈ 2,71828183
Лн као инверзна функција експоненцијалне функције
Функција природног логаритма лн (к) је инверзна функција експоненцијалне функције е к .
За к/ 0,
ф ( ф -1 ( к )) = е лн ( к ) = к
Или
ф -1 ( ф ( к )) = лн ( е к ) = к
Правила и својства природног логаритма
| Назив правила | Правило | Пример |
|---|---|---|
Правило производа |
лн ( к ∙ и ) = лн ( к ) + лн ( и ) |
лн (3 ∙ 7) = лн (3) + лн (7) |
Правило количника |
лн ( к / и ) = лн ( к ) - лн ( и ) |
лн (3 / 7) = лн (3) - лн (7) |
Правило моћи |
лн ( к и ) = и ∙ лн ( к ) |
лн (2 8 ) = 8 ∙ лн (2) |
У изведеници |
ф ( к ) = лн ( к ) ⇒ ф ' ( к ) = 1 / к | |
У интеграл |
∫ лн ( к ) дк = к ∙ (лн ( к ) - 1) + Ц. | |
У негативном броју |
лн ( к ) није дефинисано када је к ≤ 0 | |
нула |
лн (0) није дефинисано | |
У једном |
лн (1) = 0 | |
У бесконачности |
лим лн ( к ) = ∞, када је к → ∞ | |
| Ојлеров идентитет | лн (-1) = и π |
Логаритамско правило производа
Логаритам множења к и и је збир логаритма к и логаритма и.
лог б ( к ∙ и ) = лог б ( к ) + лог б ( и )
На пример:
лог 10 (3 ∙ 7) = лог 10 (3) + лог 10 (7)
Правило количника логаритма
Логаритам дељења к и и је разлика логаритма к и логаритма и.
лог б ( к / и ) = лог б ( к ) - лог б ( и )
На пример:
лог 10 (3 / 7) = лог 10 (3) - лог 10 (7)
Правило снаге логаритма
Логаритам к подигнут у степен и је и пута логаритма к.
лог б ( к и ) = и ∙ лог б ( к )
На пример:
лог 10 (2 8 ) = 8 ∙ лог 10 (2)
Дериват природног логаритма
Извод функције природног логаритма је реципрочна функција.
Када
ф ( к ) = лн ( к )
Извод ф (к) је:
ф ' ( к ) = 1 / к
Интеграл природног логаритма
Интеграл функције природног логаритма дат је:
Када
ф ( к ) = лн ( к )
Интеграл ф (к) је:
∫ ф ( к ) дк = ∫ лн ( к ) дк = к ∙ (лн ( к ) - 1) + Ц
Лн од 0
Природни логаритам нуле није дефинисан:
лн (0) није дефинисано
Граница близу 0 природног логаритма к, када се к приближи нули, је минус бесконачност:
![]()
Лн од 1
Природни логаритам један је нула:
лн (1) = 0
Лн бесконачности
Граница природног логаритма бесконачности, када се к приближава бесконачности, једнака је бесконачности:
лим лн ( к ) = ∞, када је к → ∞
Сложени логаритам
За комплексни број з:
з = ре иθ = к + ии
Сложени логаритам биће (н = ...- 2, -1,0,1,2, ...):
Лог з = лн ( р ) + и ( θ + 2нπ ) = лн (√ ( к 2 + и 2 )) + и · арктан ( и / к ))
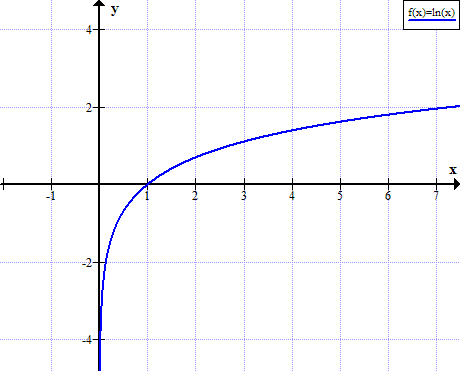
Графикон лн (к)
лн (к) није дефинисан за реалне позитивне вредности к:
Табела природних логаритама
| к | лн к |
|---|---|
| 0 | недефинисан |
| 0 + | - ∞ |
| 0.0001 | -9.210340 |
| 0,001 | -6.907755 |
| 0,01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0.693147 |
| е ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
Такође видети
- Логаритам (дневник)
- Калкулатор природног логаритма
- Природни логаритам нуле
- Природни логаритам један
- Природни логаритам е
- Природни логаритам бесконачности
- Природни логаритам негативног броја
- Лн инверзна функција
- Графикон лн (к)
- Табела природног логаритма
- Логаритамски калкулатор
- е константа