е константа
Константа или Ојлеров број је математичка константа. Е константа је стваран и ирационалан број.
е = 2.718281828459 ...
Дефиниција е
Е константа је дефинисана као ограничење:
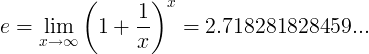
Алтернативне дефиниције
Е константа је дефинисана као ограничење:
![]()
Е константа је дефинисана као бесконачни низ:
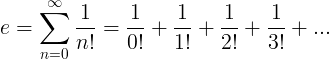
Својства е
Узајамно од е
Реципрочна вредност е је граница:
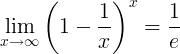
Изведени из е
Извод експоненцијалне функције је експоненцијална функција:
( е к ) '= е к
Извод функције природног логаритма је реципрочна функција:
(лог е к ) '= (лн к )' = 1 / к
Интеграли е
Неодређени интеграл експоненцијалне функције е к је експоненцијална функција е к .
∫ е к дк = е к + ц
Неодређени интеграл функције природног логаритма лог е к је:
∫ лог е к дк = ∫ лн к дк = к лн к - к + ц
Дефинитивни интеграл од 1 до е реципрочне функције 1 / к је 1:
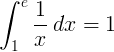
Основа е логаритам
Природни логаритам броја к дефинисан је као основни е логаритам к:
лн к = лог е к
Експоненцијална функција
Експоненцијална функција је дефинисана као:
ф ( к ) = екп ( к ) = е к
Ојлерова формула
Комплексни број е иθ има идентитет:
е иθ = цос ( θ ) + и син ( θ )
и је замишљена јединица (квадратни корен од -1).
θ је било који реалан број.
Такође видети
- Како је 2.71828183?
- Логаритамска правила
- Природни логаритам
- Правила експонената
- Нормална расподела
- Пи константа
- е константа - википедиа