Променљив

У вероватноћи и статистици, варијанса случајне променљиве је просечна вредност квадратне удаљености од средње вредности. Представља начин на који је случајна променљива распоређена у близини средње вредности. Мала варијанса указује на то да је случајна променљива распоређена у близини средње вредности. Велика варијанса указује на то да се случајна променљива дистрибуира далеко од средње вредности. На пример, уз нормалну дистрибуцију, уска крива звона имаће малу варијансу, а широка крива звона велику варијансу.

Дефиниција варијансе

Одступање случајне променљиве Кс је очекивана вредност квадрата разлике Кс и очекивана вредност μ.

σ 2 = Вар ( Кс ) = Е [( Кс - μ ) 2 ]

Из дефиниције варијансе можемо добити

σ 2 = Вар ( Кс ) = Е ( Кс 2 ) - μ 2

Одступање континуиране случајне променљиве

За континуирану случајну променљиву са средњом вредношћу μ и функцијом густине вероватноће ф (к):

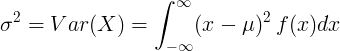
\ сигма ^ 2 = Вар (Кс) = \ инт _ {- \ инфти} ^ {\ инфти} (к- \ му) ^ 2 \: ф (к) дк

или

Вар (Кс) = \ лево [\ инт _ {- \ инфти} ^ {\ инфти} к ^ 2 \: ф (к) дк \ десно] - \ му ^ 2

Одступање дискретне случајне променљиве

За дискретну случајну променљиву Кс са средњом вредношћу μ и функцијом масе вероватноће П (к):

\ сигма ^ 2 = Вар (Кс) = \ сум_ {и} ^ {} (к_и- \ му _Кс) ^ 2П_Кс (к_и)

или

Вар (Кс) = \ лево [\ сум_ {и} ^ {} к_и ^ 2П (к_и) \ десно] - \ му ^ 2

Особине варијансе

Када су Кс и И независне случајне променљиве:

Вар ( Кс + И ) = Вар ( Кс ) + Вар ( И )

 

Стандардна девијација ►

 

Такође видети

ВЕРОВАТНОСТ И СТАТИСТИКА
БРЗЕ ТАБЛИЦЕ