Стандардна девијација

У вероватноћи и статистици, стандардна девијација случајне променљиве је просечна удаљеност случајне променљиве од средње вредности.

Представља како је случајна променљива распоређена у близини средње вредности. Мала стандардна девијација указује на то да је случајна променљива распоређена у близини средње вредности. Велика стандардна девијација указује на то да се случајна променљива дистрибуира далеко од средње вредности.

Формула дефиниције стандардног одступања

Стандардна девијација је квадратни корен варијансе случајне променљиве Кс, са средњом вредношћу μ.

\ сигма = стд (Кс) = \ скрт {Вар (Кс)} = \ скрт {Е ((Кс- \ му) ^ 2}

Из дефиниције стандардне девијације можемо доћи

\ сигма = стд (Кс) = \ скрт {Е (Кс ^ 2) - \ му ^ 2}

Стандардна девијација континуиране случајне променљиве

За континуирану случајну променљиву са средњом вредношћу μ и функцијом густине вероватноће ф (к):

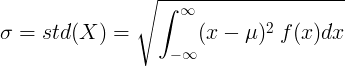
\ сигма = стд (Кс) = \ скрт {\ инт _ {- \ инфти} ^ {\ инфти} (к- \ му) ^ 2 \: ф (к) дк}

или

\ сигма = стд (Кс) = \ скрт {\ лево [\ инт _ {- \ инфти} ^ {\ инфти} к ^ 2 \: ф (к) дк \ десно] - \ му ^ 2}

Стандардна девијација дискретне случајне променљиве

За дискретну случајну променљиву Кс са средњом вредношћу μ и функцијом масе вероватноће П (к):

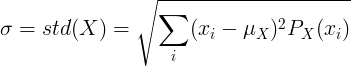
\ сигма = стд (Кс) = \ скрт {\ сум_ {и} ^ {} (к_и- \ му _Кс) ^ 2П_Кс (к_и)}

или

\ сигма = стд (Кс) = \ скрт {\ лефт [\ сум_ {и} ^ {} к_и ^ 2П (к_и) \ ригхт] - \ му ^ 2}

 

Расподела вероватноће ►

 

Такође видети

ВЕРОВАТНОСТ И СТАТИСТИКА
БРЗЕ ТАБЛИЦЕ