Расподела
У вероватноћи и статистици дистрибуција је карактеристика случајне променљиве, описује вероватноћу случајне променљиве у свакој вредности.
Свака расподела има одређену функцију густине вероватноће и функцију расподеле вероватноће.
Иако постоји неограничен број расподела вероватноће, користи се неколико уобичајених расподела.
Функција расподеле
Расподела вероватноће је описана кумулативном функцијом расподеле Ф (к),
што је вероватноћа да случајна променљива Кс добије вредност мању или једнаку к:
Ф ( к ) = П ( Кс ≤ к )
Континуирана дистрибуција
Кумулативна функција расподеле Ф (к) израчунава се интеграцијом функције густине вероватноће ф (у) континуиране случајне променљиве Кс.
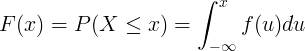
Дискретна расподела
Кумулативна функција расподеле Ф (к) израчунава се збрајањем функције вероватноће масе П (у) дискретне случајне променљиве Кс.
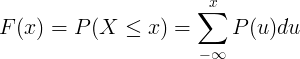
Табела континуиране дистрибуције
Континуирана расподела је расподела континуиране случајне променљиве.
Пример континуиране дистрибуције
...
Табела континуиране дистрибуције
| Назив дистрибуције | Симбол дистрибуције | Функција густине вероватноће (пдф) | Значити | Променљив |
|---|---|---|---|---|
| ф Кс ( к ) |
μ = Е ( Кс ) |
σ 2 = Вар ( Кс ) |
||
| Уобичајено / гауссиан | Кс ~ Н (μ, σ 2 ) |
|
μ | σ 2 |
| Униформ | Кс ~ У ( а , б ) |
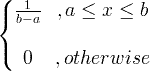 |
|
|
| Експоненцијално | Кс ~ екп (λ) | |
|
|
| Гама | Кс ~ гама ( ц , λ) | 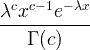 к / 0, ц / 0, λ/ 0 |
|
|
| Хи квадрат | Кс ~ χ 2 ( к ) |
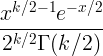 |
к |
2 к |
| Висхарт | ||||
| Ф | Кс ~ Ф ( к 1 , к 2 ) |
|||
| Бета | ||||
| Веибулл | ||||
| Лог-нормал | Кс ~ ЛН (μ, σ 2 ) |
|||
| Раилеигх | ||||
| Цауцхи | ||||
| Дирицхлет | ||||
| Лаплаце | ||||
| Наплаћивати | ||||
| Пиринач | ||||
| Студент'с т |
Табела дискретних расподела
Дискретна расподела је расподела дискретне случајне променљиве.
Пример дискретне дистрибуције
...
Табела дискретних расподела
| Назив дистрибуције | Симбол дистрибуције | Функција масе вероватноће (пмф) | Значити | Променљив | |
|---|---|---|---|---|---|
| ф к ( к ) = П ( Кс = к ) к = 0,1,2, ... |
Е ( к ) | Вар ( к ) | |||
| Бином | Кс ~ Бин ( н , п ) |
|
нп |
нп (1- п ) |
|
| Поиссон | Кс ~ Поиссон (λ) |
|
λ ≥ 0 |
λ |
λ |
| Униформ | Кс ~ У ( а, б ) |
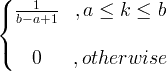 |
|
|
|
| Геометриц | Кс ~ Геом ( п ) |
|
|
|
|
| Хипер-геометријска | Кс ~ ХГ ( Н , К , н ) |
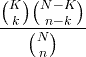 |
Н = 0,1,2, ... К = 0,1, .., Н. н = 0,1, ..., Н. |
|
|
| Берноулли | Кс ~ Берн ( п ) |
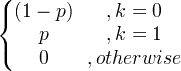 |
п |
п (1- п ) |
|
Такође видети
ВЕРОВАТНОСТ И СТАТИСТИКА
- Основна вероватноћа
- Очекивање
- Променљив
- Стандардна девијација
- Расподела
- Нормална расподела
- Статистички симболи
БРЗЕ ТАБЛИЦЕ