Основне формуле вероватноће

 

Опсег вероватноће

0 ≤ П ( А ) ≤ 1

Правило комплементарних догађаја

П ( А Ц ) + П ( А ) = 1

Правило сабирања

П (А∪Б) = П (А) + П (Б) - П (А∩Б)

Дисјуинт Евентс

Догађаји А и Б су раздвојени

П (А∩Б) = 0

Условна вероватноћа

П (А | Б) = П (А∩Б) / П (Б)

Баиес формула

П (А | Б) = П (Б | А) ⋅ П (А) / П (Б)

Независни догађаји

Догађаји А и Б су независни

П (А∩Б) = П (А) ⋅ П (Б)

Функција расподеле

Ф Кс ( к ) = П ( Кс ≤ к )

Функција масе вероватноће

збир (и = 1..н, П (Кс = к (и)) = 1

Функција густине вероватноће

фКс (к) = дФКС (к) / дк

ФКС (к) = интеграл (-инф..к, фКс (и) * ди)

ФКС (к) = збир (к = 1..к, П (Кс = к))

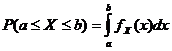
П (а <= Кс <= б) = интеграл (а..б, фКс (к) * дк)

интеграл (-инф..инф, фКс (к) * дк) = 1

 

Коваријанса

Цок (Кс, И) = Е (Кс-ук) (И-уи) = Е (КСИ) - ук * уи

Корелација

исправан (Кс, И) = Цов (Кс, И) / (Стд (Кс) * Стд (И))

 

Берноулли: 0-неуспех 1-успех

Геометријски: 0-неуспех 1-успех

Хипергеометријски: Н објеката са К објеката успеха, узето је н објеката.

 

 

 
 
ВЕРОВАТНОСТ И СТАТИСТИКА
БРЗЕ ТАБЛИЦЕ