e மாறிலி

e மாறிலி அல்லது யூலரின் எண் ஒரு கணித மாறிலி. மின் மாறிலி உண்மையான மற்றும் பகுத்தறிவற்ற எண்.

e = 2.718281828459 ...

இ வரையறை
இ இன் பண்புகள்
அடிப்படை மின் மடக்கை
அதிவேக செயல்பாடு
யூலரின் சூத்திரம்

இ வரையறை

மின் மாறிலி வரம்பாக வரையறுக்கப்படுகிறது:

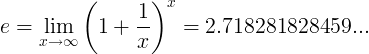
$e = \ lim_ {x \ வலதுபுறம் \ infty} \ இடது (1+ \ frac {1} {x} \ வலது) ^ x = 2.718281828459 ...$

மாற்று வரையறைகள்

மின் மாறிலி வரம்பாக வரையறுக்கப்படுகிறது:

$e = \ lim_ {x \ வலதுபுறம் 0} \ இடது (1+ \ வலது x) ^ \ frac {1} {x}$

மின் மாறிலி எல்லையற்ற தொடராக வரையறுக்கப்படுகிறது:

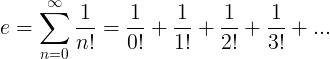
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} {. 2!} + \ Frac {1} {3!} + ...$

இ இன் பண்புகள்

மின் பரிமாற்றம்

E இன் பரஸ்பர வரம்பு:

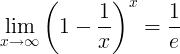
$\ lim_ {x \ வலதுபுறம் \ infty} \ இடது (1- \ frac {1} {x} \ வலது) ^ x = \ frac {1} {e}.$

இ இன் வழித்தோன்றல்கள்

அதிவேக செயல்பாட்டின் வழித்தோன்றல் அதிவேக செயல்பாடு:

( e ^x ) '= e ^x

இயற்கையான மடக்கை செயல்பாட்டின் வழித்தோன்றல் பரஸ்பர செயல்பாடு:

(பதிவு _e x ) '= (ln x )' = 1 / x

மின் ஒருங்கிணைப்புகள்

அதிவேக செயல்பாட்டின் காலவரையற்ற ஒருங்கிணைப்பு e ^x என்பது அதிவேக செயல்பாடு e ^{x ஆகும்} .

∫ e ^x dx = e ^x + c

இயற்கை மடக்கை செயல்பாடு பதிவு _e x இன் காலவரையற்ற ஒருங்கிணைப்பு :

∫ log _e x dx = ∫ ln x dx = x ln x - x + c

1 / x பரஸ்பர செயல்பாட்டின் 1 முதல் e வரையிலான திட்டவட்டமான ஒருங்கிணைப்பு 1:

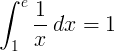
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

அடிப்படை மின் மடக்கை

ஒரு எண்ணின் இயல்பான மடக்கை x இன் அடிப்படை மின் மடக்கை என வரையறுக்கப்படுகிறது:

ln x = log _e x

அதிவேக செயல்பாடு

அதிவேக செயல்பாடு பின்வருமாறு வரையறுக்கப்படுகிறது:

f ( x ) = exp ( x ) = e ^x

யூலரின் சூத்திரம்

சிக்கலான எண் e ^iθ அடையாளத்தைக் கொண்டுள்ளது:

இ ^iθ = காஸ் ( θ ) + நான் பாவம் ( θ )

நான் கற்பனை அலகு (-1 இன் சதுர வேர்).

Any எந்த உண்மையான எண்ணும்.