அடுக்கு விதிகள்

அதிவேக விதிகள், அடுக்கு சட்டங்கள் மற்றும் எடுத்துக்காட்டுகள்.

ஒரு அடுக்கு என்றால் என்ன

N இன் சக்திக்கு உயர்த்தப்பட்ட அடிப்படை a, n மடங்குகளின் பெருக்கத்திற்கு சமம்:

a n = a × a × ... × a

                    n முறை

a என்பது அடிப்படை மற்றும் n என்பது அடுக்கு.

எடுத்துக்காட்டுகள்

3 1 = 3

3 2 = 3 × 3 = 9

3 3 = 3 × 3 × 3 = 27

3 4 = 3 × 3 × 3 × 3 = 81

3 5 = 3 × 3 × 3 × 3 × 3 = 243

எக்ஸ்போனெண்ட்ஸ் விதிகள் மற்றும் பண்புகள்

விதி பெயர் விதி உதாரணமாக
தயாரிப்பு விதிகள் ஒரு N ⋅ ஒரு மீ = ஒரு n + m 2 3 ⋅ 2 4 = 2 3 + 4 = 128
ஒரு N ⋅ ஆ N = ( ஒரு ⋅ ஆ ) , n 3 2 ⋅ 4 2 = (3⋅4) 2 = 144
அளவு விதிகள் a n / a m = a n - m 2 5 /2 3 = 2 5-3 = 4
a n / b n = ( a / b ) n 4 3 /2 3 = (4/2) 3 = 8
சக்தி விதிகள் ( b n ) m = b n⋅m (2 3 ) 2 = 2 3⋅2 = 64
b n m = b ( n m ) 2 3 2 = 2 ( 3 2 ) = 512
m √ ( b n ) = b n / m 2 (2 6 ) = 2 6/2 = 8
b 1 / n = n √ b 8 1/3 = 3 √ 8 = 2
எதிர்மறை அடுக்கு b -n = 1 / b n 2 -3 = 1/2 3 = 0.125
பூஜ்ஜிய விதிகள் b 0 = 1 5 0 = 1
0 n = 0, n / 0 க்கு 0 5 = 0
ஒரு விதிகள் b 1 = b 5 1 = 5
1 n = 1 1 5 = 1
கழித்தல் ஒரு விதி 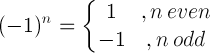(-1) 5 = -1
வழித்தோன்றல் விதி ( x n ) ' = n ⋅ x n -1 ( x 3 ) ' = 3⋅ x 3-1
ஒருங்கிணைந்த விதி ∫ எக்ஸ் N டிஎக்ஸ் = எக்ஸ் N +1 ஐ / ( N +1 ஐ) + சி ∫ எக்ஸ் 2 டிஎக்ஸ் = எக்ஸ் 2 +1 / (2 +1) + சி

தயாரிப்பு விதிகள்

ஒரே தளத்துடன் தயாரிப்பு விதி

ஒரு N ⋅ ஒரு மீ = ஒரு n + m

உதாரணமாக:

2 3 2 4 = 2 3 + 4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128

அதே அடுக்குடன் தயாரிப்பு விதி

ஒரு N ⋅ ஆ N = ( ஒரு ⋅ ஆ ) , n

உதாரணமாக:

3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 12⋅12 = 144

காண்க: பெருக்கிகள் அடுக்கு

சொற்பொழிவாளர்கள் மேற்கோள் விதிகள்

ஒரே தளத்துடன் கூடிய அளவு விதி

a n / a m = a n - m

உதாரணமாக:

2 5 /2 3 = 2 5-3 = 2 2 = 2⋅2 = 4

அதே அடுக்குடன் அளவு விதி

a n / b n = ( a / b ) n

உதாரணமாக:

4 3 /2 3 = (4/2) 3 = 2 3 = 2⋅2⋅2 = 8

காண்க: எக்ஸ்போனென்ட்களைப் பிரித்தல்

சக்தி விதிகள்

சக்தி விதி I.

( a n ) m = a n⋅m

உதாரணமாக:

(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64

சக்தி விதி II

a n m = a ( n m )

உதாரணமாக:

2 3 2 = 2 (3 2 ) = 2 (3⋅3) = 2 9 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512

தீவிரவாதிகளுடன் சக்தி ஆட்சி

m √ ( a n ) = a n / m

உதாரணமாக:

2 (2 6 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8

எதிர்மறை எக்ஸ்போனெண்டுகள் ஆட்சி

b -n = 1 / b n

உதாரணமாக:

2 -3 = 1/2 3 = 1 / (2⋅2⋅2) = 1/8 = 0.125

காண்க: எதிர்மறை அடுக்கு

 

அடுக்கு கால்குலேட்டர்

 

மேலும் காண்க

எண்கள்
விரைவான அட்டவணைகள்