மாறுபாடு
நிகழ்தகவு மற்றும் புள்ளியியலில், மாறுபாடு ஒரு சீரற்ற மாறி சராசரி மதிப்பு இருந்து சதுர தூரத்தில் சராசரி மதிப்பு உள்ளது. சராசரி மதிப்புக்கு அருகில் சீரற்ற மாறி எவ்வாறு விநியோகிக்கப்படுகிறது என்பதை இது குறிக்கிறது. சிறிய மாறுபாடு சீரற்ற மாறி சராசரி மதிப்புக்கு அருகில் விநியோகிக்கப்படுவதைக் குறிக்கிறது. சீரற்ற மாறி சராசரி மதிப்பிலிருந்து வெகு தொலைவில் விநியோகிக்கப்படுவதை பெரிய மாறுபாடு குறிக்கிறது. எடுத்துக்காட்டாக, சாதாரண விநியோகத்துடன், குறுகிய மணி வளைவு சிறிய மாறுபாட்டைக் கொண்டிருக்கும் மற்றும் பரந்த மணி வளைவு பெரிய மாறுபாட்டைக் கொண்டிருக்கும்.
மாறுபாடு வரையறை
சீரற்ற மாறி X இன் மாறுபாடு என்பது X இன் வேறுபாட்டின் சதுரங்களின் எதிர்பார்க்கப்பட்ட மதிப்பு மற்றும் எதிர்பார்க்கப்படும் மதிப்பு μ ஆகும்.
σ 2 = மாறிலி ( எக்ஸ் ) = மின் [( எக்ஸ் - μ ) 2 ]
மாறுபாட்டின் வரையறையிலிருந்து நாம் பெறலாம்
σ 2 = மாறிலி ( எக்ஸ் ) = மின் ( எக்ஸ் 2 ) - μ 2
தொடர்ச்சியான சீரற்ற மாறியின் மாறுபாடு
சராசரி மதிப்பு μ மற்றும் நிகழ்தகவு அடர்த்தி செயல்பாடு f (x) உடன் தொடர்ச்சியான சீரற்ற மாறிக்கு:
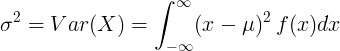
அல்லது
![Var (X) = \ இடது [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2](variance/cont_var2.gif)
தனித்துவமான சீரற்ற மாறியின் மாறுபாடு
சராசரி மதிப்பு μ மற்றும் நிகழ்தகவு நிறை செயல்பாடு P (x) உடன் தனித்துவமான சீரற்ற மாறி X க்கு:
![]()
அல்லது
![Var (X) = \ இடது [\ sum_ {i} ^ {x_i ^ 2P (x_i) \ வலது] - \ mu ^ 2](variance/disc_var2.gif)
மாறுபாட்டின் பண்புகள்
எக்ஸ் மற்றும் ஒய் சுயாதீனமான சீரற்ற மாறிகள் போது:
Var ( X + Y ) = Var ( X ) + Var ( Y )
மேலும் காண்க
நிகழ்தகவு மற்றும் புள்ளிவிவரங்கள்
- அடிப்படை நிகழ்தகவு
- எதிர்பார்ப்பு
- மாறுபாடு
- நிலையான விலகல்
- நிகழ்தகவு விநியோகம்
- இயல்பான விநியோகம்
- புள்ளிவிவர சின்னங்கள்
விரைவான அட்டவணைகள்