వైవిధ్యం
సంభావ్యత మరియు గణాంకాలలో, యాదృచ్ఛిక వేరియబుల్ యొక్క వైవిధ్యం సగటు విలువ నుండి చదరపు దూరం యొక్క సగటు విలువ. ఇది యాదృచ్ఛిక వేరియబుల్ సగటు విలువకు సమీపంలో ఎలా పంపిణీ చేయబడుతుందో సూచిస్తుంది. యాదృచ్ఛిక వేరియబుల్ సగటు విలువ దగ్గర పంపిణీ చేయబడిందని చిన్న వ్యత్యాసం సూచిస్తుంది. యాదృచ్ఛిక వేరియబుల్ సగటు విలువకు దూరంగా పంపిణీ చేయబడిందని పెద్ద వైవిధ్యం సూచిస్తుంది. ఉదాహరణకు, సాధారణ పంపిణీతో, ఇరుకైన బెల్ కర్వ్ చిన్న వ్యత్యాసాన్ని కలిగి ఉంటుంది మరియు విస్తృత బెల్ కర్వ్ పెద్ద వ్యత్యాసాన్ని కలిగి ఉంటుంది.
వ్యత్యాస నిర్వచనం
యాదృచ్ఛిక వేరియబుల్ X యొక్క వైవిధ్యం X యొక్క వ్యత్యాసం యొక్క చతురస్రాల యొక్క అంచనా విలువ మరియు value హించిన విలువ μ.
σ 2 = Var ( X ) = E [( X - μ ) 2 ]
వైవిధ్యం యొక్క నిర్వచనం నుండి మనం పొందవచ్చు
σ 2 = Var ( X ) = E ( X 2 ) - μ 2
నిరంతర రాండమ్ వేరియబుల్ యొక్క వైవిధ్యం
సగటు విలువ μ మరియు సంభావ్యత సాంద్రత ఫంక్షన్ f (x) తో నిరంతర యాదృచ్ఛిక వేరియబుల్ కోసం:
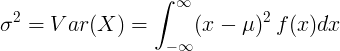
లేదా
![Var (X) = \ ఎడమ [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2](variance/cont_var2.gif)
వివిక్త రాండమ్ వేరియబుల్ యొక్క వైవిధ్యం
సగటు విలువ μ మరియు సంభావ్యత ద్రవ్యరాశి ఫంక్షన్ P (x) తో వివిక్త రాండమ్ వేరియబుల్ X కోసం:
![]()
లేదా
![Var (X) = \ ఎడమ [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ కుడి] - \ mu ^ 2](variance/disc_var2.gif)
వైవిధ్యం యొక్క లక్షణాలు
X మరియు Y స్వతంత్ర యాదృచ్ఛిక వేరియబుల్స్ అయినప్పుడు:
Var ( X + Y ) = Var ( X ) + Var ( Y )
ఇది కూడ చూడు
సంభావ్యత & గణాంకాలు
- ప్రాథమిక సంభావ్యత
- నిరీక్షణ
- వైవిధ్యం
- ప్రామాణిక విచలనం
- సంభావ్యత పంపిణి
- సాధారణ పంపిణీ
- గణాంకాలు చిహ్నాలు
రాపిడ్ టేబుల్స్