సంభావ్యత పంపిణి
సంభావ్యత మరియు గణాంకాల పంపిణీలో యాదృచ్ఛిక వేరియబుల్ యొక్క లక్షణం, ప్రతి విలువలో యాదృచ్ఛిక వేరియబుల్ యొక్క సంభావ్యతను వివరిస్తుంది.
ప్రతి పంపిణీకి నిర్దిష్ట సంభావ్యత సాంద్రత ఫంక్షన్ మరియు సంభావ్యత పంపిణీ ఫంక్షన్ ఉంటుంది.
సంభావ్యత పంపిణీల యొక్క నిరవధిక సంఖ్య ఉన్నప్పటికీ, ఉపయోగంలో అనేక సాధారణ పంపిణీలు ఉన్నాయి.
సంచిత పంపిణీ ఫంక్షన్
సంభావ్యత పంపిణీని సంచిత పంపిణీ ఫంక్షన్ F (x) వివరిస్తుంది,
ఇది x కంటే చిన్న లేదా సమానమైన విలువను పొందడానికి యాదృచ్ఛిక వేరియబుల్ X యొక్క సంభావ్యత:
F ( x ) = P ( X ≤ x )
నిరంతర పంపిణీ
నిరంతర యాదృచ్ఛిక వేరియబుల్ X యొక్క సంభావ్యత సాంద్రత ఫంక్షన్ f (u) యొక్క ఏకీకరణ ద్వారా సంచిత పంపిణీ ఫంక్షన్ F (x) లెక్కించబడుతుంది.
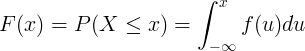
వివిక్త పంపిణీ
సంచిత పంపిణీ ఫంక్షన్ F (x) వివిక్త రాండమ్ వేరియబుల్ X యొక్క సంభావ్యత ద్రవ్యరాశి ఫంక్షన్ P (u) యొక్క సమ్మషన్ ద్వారా లెక్కించబడుతుంది.
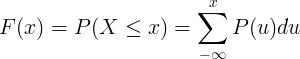
నిరంతర పంపిణీ పట్టిక
నిరంతర పంపిణీ అనేది నిరంతర రాండమ్ వేరియబుల్ యొక్క పంపిణీ.
నిరంతర పంపిణీ ఉదాహరణ
...
నిరంతర పంపిణీ పట్టిక
| పంపిణీ పేరు | పంపిణీ చిహ్నం | సంభావ్యత సాంద్రత ఫంక్షన్ (పిడిఎఫ్) | అర్థం | వైవిధ్యం |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| సాధారణ / గాస్సియన్ | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| ఏకరీతి | X ~ U ( a , b ) |
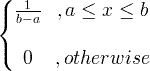 |
|
|
| ఘాతాంకం | X ~ exp () | |
|
|
| గామా | X ~ గామా ( సి ,) | 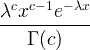 x / 0, సి / 0, λ/ 0 |
|
|
| చి స్క్వేర్ | X ~ χ 2 ( క ) |
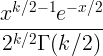 |
k |
2 క |
| విషార్ట్ | ||||
| ఎఫ్ | X ~ F ( k 1 , k 2 ) |
|||
| బీటా | ||||
| వీబుల్ | ||||
| లాగ్-సాధారణ | X ~ LN (μ, σ 2 ) |
|||
| రేలీ | ||||
| కౌచీ | ||||
| డిరిచ్లెట్ | ||||
| లాప్లేస్ | ||||
| లెవీ | ||||
| బియ్యం | ||||
| విద్యార్థి టి |
వివిక్త పంపిణీ పట్టిక
వివిక్త పంపిణీ అనేది వివిక్త రాండమ్ వేరియబుల్ యొక్క పంపిణీ.
వివిక్త పంపిణీ ఉదాహరణ
...
వివిక్త పంపిణీ పట్టిక
| పంపిణీ పేరు | పంపిణీ చిహ్నం | సంభావ్యత మాస్ ఫంక్షన్ (pmf) | అర్థం | వైవిధ్యం | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | వర్ ( x ) | |||
| ద్విపద | X ~ బిన్ ( n , p ) |
|
np |
np (1- పే ) |
|
| పాయిజన్ | X ~ పాయిసన్ (λ) |
|
λ 0 |
λ |
λ |
| ఏకరీతి | X ~ U ( a, b ) |
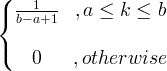 |
|
|
|
| రేఖాగణిత | X ~ జియోమ్ ( p ) |
|
|
|
|
| హైపర్-రేఖాగణిత | X ~ HG ( N , K , n ) |
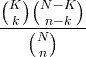 |
ఎన్ = 0,1,2, ... కె = 0,1, .., ఎన్ n = 0,1, ..., ఎన్ |
|
|
| బెర్నౌల్లి | X ~ బెర్న్ ( p ) |
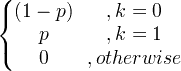 |
p |
p (1- పే ) |
|
ఇది కూడ చూడు
సంభావ్యత & గణాంకాలు
- ప్రాథమిక సంభావ్యత
- నిరీక్షణ
- వైవిధ్యం
- ప్రామాణిక విచలనం
- సంభావ్యత పంపిణి
- సాధారణ పంపిణీ
- గణాంకాలు చిహ్నాలు
రాపిడ్ టేబుల్స్