ప్రాథమిక సంభావ్యత సూత్రాలు

 

సంభావ్యత పరిధి

0 ≤ పి ( ఎ ) 1

కాంప్లిమెంటరీ ఈవెంట్స్ నియమం

పి ( ఎ సి ) + పి ( ఎ ) = 1

చేరిక నియమం

P (A∪B) = P (A) + P (B) - P (A∩B)

ఈవెంట్లను విడదీయండి

A మరియు B సంఘటనలు iff

P (A∩B) = 0

షరతులతో కూడిన సంభావ్యత

P (A | B) = P (A∩B) / P (B)

బేయస్ ఫార్ములా

పి (ఎ ​​| బి) = పి (బి | ఎ) ⋅ పి (ఎ) / పి (బి)

స్వతంత్ర సంఘటనలు

A మరియు B సంఘటనలు స్వతంత్రంగా ఉంటే

P (A∩B) = P (A) ⋅ P (B)

సంచిత పంపిణీ ఫంక్షన్

F X ( X ) = P ( X ≤ x )

సంభావ్యత మాస్ ఫంక్షన్

sum (i = 1..n, P (X = x (i)) = 1

సంభావ్యత సాంద్రత ఫంక్షన్

fX (x) = dFX (x) / dx

FX (x) = సమగ్ర (-inf..x, fX (y) * dy)

FX (x) = sum (k = 1..x, P (X = k))

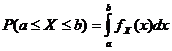
P (a <= X <= b) = సమగ్ర (a..b, fX (x) * dx)

సమగ్ర (-inf..inf, fX (x) * dx) = 1

 

కోవియారిన్స్

కాక్స్ (X, Y) = E (X-ux) (Y-uy) = E (XY) - ux * uy

సహసంబంధం

corr (X, Y) = Cov (X, Y) / (Std (X) * Std (Y))

 

బెర్నౌల్లి: 0-వైఫల్యం 1-విజయం

రేఖాగణిత: 0-వైఫల్యం 1-విజయం

హైపర్జియోమెట్రిక్: K విజయ వస్తువులతో N వస్తువులు, n వస్తువులు తీసుకోబడతాయి.

 

 

 
 
సంభావ్యత & గణాంకాలు
రాపిడ్ టేబుల్స్