Цілісний

Інтеграція - це зворотна операція виведення.

Інтеграл функції - це область під графіком функції.

Невизначене інтегральне визначення

Коли dF (x) / dx = f (x) =/ інтеграл (f (x) * dx) = F (x) + c

Невизначені інтегральні властивості

інтеграл (f (x) + g (x)) * dx = інтеграл (f (x) * dx) + інтеграл (g (x) * dx)

інтеграл (a * f (x) * dx) = a * інтеграл (f (x) * dx)

інтеграл (f (a * x) * dx) = 1 / a * F (a * x) + c

інтеграл (f (x + b) * dx) = F (x + b) + c

інтеграл (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

інтеграл (df (x) / dx * dx) = f (x)

Зміна змінної інтеграції

Колиx = g (t) іdx = g '(t) * dt

інтеграл (f (x) * dx) = інтеграл (f (g (t)) * g '(t) * dt)

Інтеграція за частинами

інтеграл (f (x) * g '(x) * dx) = f (x) * g (x) - інтеграл (f' (x) * g (x) * dx)

Таблиця інтегралів

інтеграл (f (x) * dx = F (x) + c

інтеграл (a * dx) = a * x + c

інтеграл (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, коли a </ - 1

інтеграл (1 / x * dx) = ln (abs (x)) + c

інтеграл (e ^ x * dx) = e ^ x + c

інтеграл (a ^ x * dx) = a ^ x / ln (x) + c

інтеграл (ln (x) * dx) = x * ln (x) - x + c

інтеграл (sin (x) * dx) = -cos (x) + c

інтеграл (cos (x) * dx) = sin (x) + c

інтеграл (tan (x) * dx) = -ln (abs (cos (x))) + c

інтеграл (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

інтеграл (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

інтеграл (арктан (x) * dx) = x * арктан (x) - 1/2 * ln (1 + x ^ 2) + c

інтеграл (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

інтеграл (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

інтеграл (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

інтеграл (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

інтеграл (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * арктан (x / a) + c

інтеграл (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

інтеграл (sinh (x) * dx) = cosh (x) + c

інтеграл (cosh (x) * dx) = sinh (x) + c

інтеграл (tanh (x) * dx) = ln (cosh (x)) + c

 

Певне інтегральне визначення

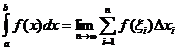
інтеграл (a..b, f (x) * dx) = lim (n-/ inf, сума (i = 1..n, f (z (i)) * dx (i))) 

Колиx0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Певний інтегральний розрахунок

Коли ,

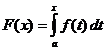 dF (x) / dx = f (x) і

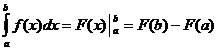
інтеграл (a..b, f (x) * dx) = F (b) - F (a) 

Певні інтегральні властивості

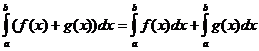
інтеграл (a..b, (f (x) + g (x)) * dx) = інтеграл (a..b, f (x) * dx) + інтеграл (a..b, g (x) * dx )

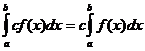
інтеграл (a..b, c * f (x) * dx) = c * інтеграл (a..b, f (x) * dx)

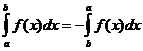
інтеграл (a..b, f (x) * dx) = - інтеграл (b..a, f (x) * dx)

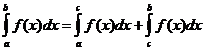
інтеграл (a..b, f (x) * dx) = інтеграл (a..c, f (x) * dx) + інтеграл (c..b, f (x) * dx)

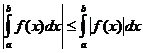
abs (інтеграл (a..b, f (x) * dx)) <= інтеграл (a..b, abs (f (x)) * dx)

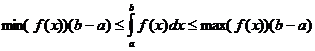хв (f (x)) * (ba) <= інтеграл (a..b, f (x) * dx) <= max (f (x)) * (ba) колиx член [a, b]

Зміна змінної інтеграції

Колиx = g (t) ,dx = g '(t) * dt ,g (альфа) = a ,g (бета) = b

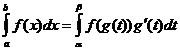
інтеграл (a..b, f (x) * dx) = інтеграл (альфа..бета, f (g (t)) * g '(t) * dt)

Інтеграція за частинами

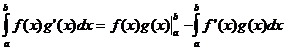
інтеграл (a..b, f (x) * g '(x) * dx) = інтеграл (a..b, f (x) * g (x) * dx) - інтеграл (a..b, f' (x) * g (x) * dx)

Теорема про середнє значення

Коли f ( x ) неперервна, існує точкаc є членом [a, b] тому

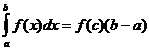
інтеграл (a..b, f (x) * dx) = f (c) * (ba)  

Трапецієподібне наближення певного інтеграла

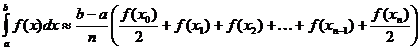
інтеграл (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

Гамма-функція

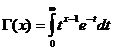
гамма (x) = інтеграл (0..inf, t ^ (x-1) * e ^ (- t) * dt

Функція гамми збіжна при x/ 0 .

Властивості гамма-функції

G ( x +1) = x G ( x )

G ( n +1) = n ! , коли n ℕ (додатне ціле число).є членом

Бета-функція

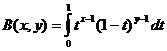
B (x, y) = інтеграл (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Бета-функція та співвідношення гамма-функцій

B (x, y) = Гама (x) * Гама (y) / Гама (x + y)

 

 

 

КАЛКУЛ
ШВИДКІ СТОЛИ