Дисперсія

За ймовірністю та статистикою дисперсія випадкової величини є середнім значенням квадратної відстані від середнього значення. Він представляє спосіб розподілу випадкової величини поблизу середнього значення. Мала дисперсія вказує на те, що випадкова величина розподілена поблизу середнього значення. Велика дисперсія вказує на те, що випадкова величина розподілена далеко від середнього значення. Наприклад, при нормальному розподілі вузька крива дзвона матиме малу дисперсію, а широка крива дзвоника матиме велику дисперсію.

Визначення дисперсії

Дисперсія випадкової величини X - це очікуване значення квадратів різниці X та очікуване значення μ.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

З визначення дисперсії ми можемо отримати

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Дисперсія неперервної випадкової величини

Для неперервної випадкової величини із середнім значенням μ та функцією щільності ймовірності f (x):

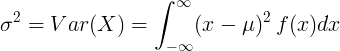
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

або

Var (X) = \ зліва [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2

Дисперсія дискретної випадкової величини

Для дискретної випадкової величини X із середнім значенням μ та функцією маси ймовірності P (x):

\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

або

Var (X) = \ зліва [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ справа] - \ mu ^ 2

Властивості дисперсії

Коли X і Y є незалежними випадковими величинами:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

Стандартне відхилення ►

 

Дивіться також

ІМОВІРНІСТЬ І СТАТИСТИКА
ШВИДКІ СТОЛИ