Стандартне відхилення

У вірогідності та статистиці стандартним відхиленням випадкової величини є середня відстань випадкової величини від середнього значення.

Він представляє, як випадкова величина розподіляється поблизу середнього значення. Невелике стандартне відхилення вказує на те, що випадкова величина розподілена поблизу середнього значення. Велике стандартне відхилення вказує на те, що випадкова величина розподілена далеко від середнього значення.

Формула визначення стандартного відхилення

Стандартне відхилення - це квадратний корінь дисперсії випадкової величини X із середнім значенням μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

З визначення стандартного відхилення ми можемо отримати

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Стандартне відхилення неперервної випадкової величини

Для неперервної випадкової величини із середнім значенням μ та функцією щільності ймовірності f (x):

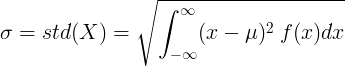
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

або

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Стандартне відхилення дискретної випадкової величини

Для дискретної випадкової величини X із середнім значенням μ та функцією маси ймовірності P (x):

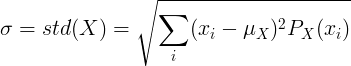
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

або

\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2}

 

Розподіл ймовірностей ►

 

Дивіться також

ІМОВІРНІСТЬ І СТАТИСТИКА
ШВИДКІ СТОЛИ