Розподіл ймовірностей
За ймовірністю та статистикою розподіл є характеристикою випадкової величини, описує ймовірність випадкової величини для кожного значення.
Кожен розподіл має певну функцію щільності ймовірності та функцію розподілу ймовірностей.
Хоча існує невизначена кількість розподілів ймовірностей, використовується кілька загальних розподілів.
Функція кумулятивного розподілу
Розподіл ймовірностей описується кумулятивною функцією розподілу F (x),
що є ймовірністю випадкової величини X отримати значення менше або рівне x:
F ( x ) = P ( X ≤ x )
Безперервний розподіл
Кумулятивна функція розподілу F (x) обчислюється інтегруванням функції щільності ймовірності f (u) неперервної випадкової величини X.
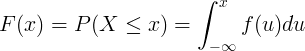
Дискретний розподіл
Кумулятивна функція розподілу F (x) обчислюється підсумовуванням функції масової ймовірності P (u) дискретної випадкової величини X.
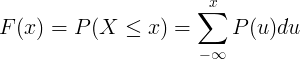
Таблиця безперервних розподілів
Безперервний розподіл - це розподіл неперервної випадкової величини.
Приклад безперервного розподілу
...
Таблиця безперервних розподілів
| Назва розповсюдження | Символ розподілу | Функція щільності ймовірності (pdf) | Середній | Дисперсія |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Звичайна / гауссова | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Уніформа | X ~ U ( a , b ) |
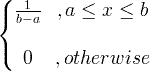 |
|
|
| Експоненціальна | X ~ exp (λ) | |
|
|
| Гамма | X ~ гамма ( c , λ) | 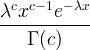 x / 0, c / 0, λ/ 0 |
|
|
| Квадрат хі | X ~ χ 2 ( k ) |
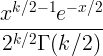 |
k |
2 к |
| Вішарт | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Бета | ||||
| Вейбулл | ||||
| Журнал-нормальний | X ~ LN (μ, σ 2 ) |
|||
| Релі | ||||
| Коші | ||||
| Діріхле | ||||
| Лапласа | ||||
| Леві | ||||
| Рис | ||||
| Студентський т |
Таблиця дискретних розподілів
Дискретний розподіл - це розподіл дискретної випадкової величини.
Приклад дискретного розподілу
...
Таблиця дискретних розподілів
| Назва розповсюдження | Символ розподілу | Функція маси ймовірності (pmf) | Середній | Дисперсія | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Двочленна | X ~ Кошик ( n , p ) |
|
np |
np (1- p ) |
|
| Пуассон | X ~ Пуассон (λ) |
|
λ ≥ 0 |
λ |
λ |
| Уніформа | X ~ U ( a, b ) |
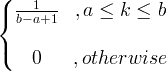 |
|
|
|
| Геометричні | X ~ Geom ( p ) |
|
|
|
|
| Гіпергеометричний | X ~ HG ( N , K , n ) |
 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Бернуллі | X ~ Берн ( p ) |
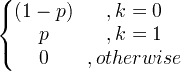 |
p |
p (1- p ) |
|
Дивіться також
ІМОВІРНІСТЬ І СТАТИСТИКА
- Базова ймовірність
- Очікування
- Дисперсія
- Стандартне відхилення
- Розподіл ймовірностей
- Нормальний розподіл
- Статистика символів
ШВИДКІ СТОЛИ