Основні формули ймовірності
Діапазон ймовірностей
0 ≤ P ( A ) ≤ 1
Правило додаткових подій
P ( A C ) + P ( A ) = 1
Правило додавання
P (A∪B) = P (A) + P (B) - P (A∩B)
Несумісні події
Події А і В несумісні між собою
P (A∩B) = 0
Умовна ймовірність
P (A | B) = P (A∩B) / P (B)
Формула Байєса
P (A | B) = P (B | A) ⋅ P (A) / P (B)
Незалежні заходи
Події A та B є незалежними
P (A∩B) = P (A) ⋅ P (B)
Функція кумулятивного розподілу
F X ( x ) = P ( X ≤ x )
Масова функція ймовірності
![]()
Функція щільності ймовірності
![]()
![]()
![]()
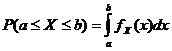
![]()
Коваріація
![]()
Співвідношення
![]()
Бернуллі: 0-невдача 1-успіх
Геометричні: 0-невдача 1-успіх
Гіпергеометричні: береться N об’єктів з K об’єктами успіху, п об’єктів.
ІМОВІРНІСТЬ І СТАТИСТИКА
- Базова ймовірність
- Очікування
- Дисперсія
- Стандартне відхилення
- Розподіл ймовірностей
- Нормальний розподіл
- Статистика символів