積分

積分是推導的逆運算。

函數的積分是函數圖下的面積。

不定積分定義

什麼時候 dF（x）/ dx = f（x）=/積分（f（x）* dx）= F（x）+ c

不定積分性質

積分（f（x）+ g（x））* dx =積分（f（x）* dx）+積分（g（x）* dx）

積分（a * f（x）* dx）= a *積分（f（x）* dx）

積分（f（a * x）* dx）= 1 / a * F（a * x）+ c

積分（f（x + b）* dx）= F（x + b）+ c

積分（f（a * x + b）* dx）= 1 / a * F（a * x + b）+ c

積分（df（x）/ dx * dx）= f（x）

積分變量的變化

什麼時候x = g（t） 和dx = g'（t）* dt

積分（f（x）* dx）=積分（f（g（t））* g'（t）* dt）

零件集成

積分（f（x）* g'（x）* dx）= f（x）* g（x）-積分（f'（x）* g（x）* dx）

積分錶

積分（f（x）* dx = F（x）+ c

積分（a * dx）= a * x + c

當a </-1時，積分（x ^ n * dx）= 1 /（a + 1）* x ^（a + 1）+ c

積分（1 / x * dx）= ln（abs（x））+ c

積分（e ^ x * dx）= e ^ x + c

積分（a ^ x * dx）= a ^ x / ln（x）+ c

積分（ln（x）* dx）= x * ln（x）-x + c

積分（sin（x）* dx）= -cos（x）+ c

積分（cos（x）* dx）= sin（x）+ c

積分（tan（x）* dx）= -ln（abs（cos（x）））+ c

積分（arcsin（x）* dx）= x * arcsin（x）+ sqrt（1-x ^ 2）+ c

積分（arccos（x）* dx）= x * arccos（x）-sqrt（1-x ^ 2）+ c

積分（arctan（x）* dx）= x * arctan（x）-1/2 * ln（1 + x ^ 2）+ c

積分（dx /（ax + b））= 1 / a * ln（abs（a * x + b））+ c

積分（1 / sqrt（a ^ 2-x ^ 2）* dx）= arcsin（x / a）+ c

積分（1 / sqrt（x ^ 2 +-a ^ 2）* dx）= ln（abs（x + sqrt（x ^ 2 +-a ^ 2））+ c

積分（x * sqrt（x ^ 2-a ^ 2）* dx）= 1 /（a * arccos（x / a））+ c

積分（1 /（a ^ 2 + x ^ 2）* dx）= 1 / a * arctan（x / a）+ c

積分（1 /（a ^ 2-x ^ 2）* dx）= 1 / 2a * ln（abs（（（（a + x）/（ax））））+ c

積分（sinh（x）* dx）= cosh（x）+ c

積分（cosh（x）* dx）= sinh（x）+ c

積分（tanh（x）* dx）= ln（cosh（x））+ c

 

定積分定義

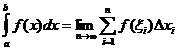
積分（a..b，f（x）* dx）= lim（n-/ inf，sum（i = 1..n，f（z（i））* dx（i）））） 

什麼時候x0 = a，xn = b

dx（k）= x（k）-x（k-1）

x（k-1）<= z（k）<= x（k）

定積分計算

什麼時候 ，

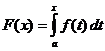 dF（x）/ dx = f（x） 和

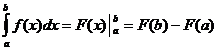
積分（a..b，f（x）* dx）= F（b）-F（a） 

定積分性質

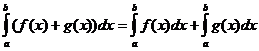
積分（a..b，（f（x）+ g（x））* dx）=積分（a..b，f（x）* dx）+積分（a..b，g（x）* dx ）

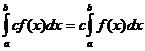
積分（a..b，c * f（x）* dx）= c *積分（a..b，f（x）* dx）

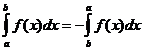
積分（a..b，f（x）* dx）=-積分（b..a，f（x）* dx）

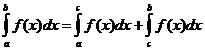
積分（a..b，f（x）* dx）=積分（a..c，f（x）* dx）+積分（c..b，f（x）* dx）

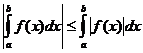
abs（積分（a..b，f（x）* dx））<=積分（a..b，abs（f（x））* dx）

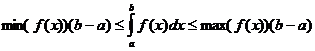min（f（x））*（ba）<=積分（a..b，f（x）* dx）<= max（f（x））*（ba） 什麼時候x [a，b]的成員

積分變量的變化

什麼時候x = g（t） ，dx = g'（t）* dt ，g（α）= a ，g（β）= b

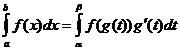
積分（a..b，f（x）* dx）=積分（alpha.beta，f（g（t））* g'（t）* dt）

零件集成

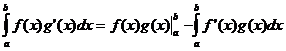
積分（a..b，f（x）* g'（x）* dx）=積分（a..b，f（x）* g（x）* dx）-積分（a..b，f' （x）* g（x）* dx）

均值定理

當f（x）連續時，有一個點c是[a，b]的成員 所以

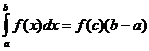
積分（a..b，f（x）* dx）= f（c）*（ba）  

定積分的梯形逼近

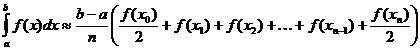
積分（a..b，f（x）* dx）〜（ba）/ n *（f（x（0））/ 2 + f（x（1））+ f（x（2））+。 。+ f（x（n-1））+ f（x（n））/ 2）

伽瑪函數

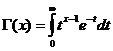
γ（x）=積分（0..inf，t ^（x-1）* e ^（-t）* dt

對於x/ 0，Gamma函數收斂。

伽瑪函數屬性

G （x +1）= x G （x ）

G （n +1）= n ！， 當Ñ ℕ （正整數）。是的成員

Beta功能

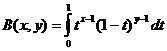
B（x，y）=積分（0..1，t ^（n-1）*（1-t）^（y-1）* dt

Beta函數和Gamma函數關係

B（x，y）=伽瑪（x）*伽瑪（y）/伽瑪（x + y）

 

 

 

結石
快速表格