ثابت البريد

ثابت e أو رقم أويلر ثابت رياضي. الثابت e هو رقم حقيقي وغير نسبي.

ه = 2.718281828459 ...

تعريف e
خصائص البريد
قاعدة e اللوغاريتم
دالة أسية
صيغة أويلر

تعريف e

يتم تعريف ثابت e على أنه الحد:

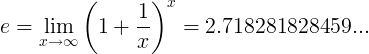
$e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...$

التعريفات البديلة

يتم تعريف ثابت e على أنه الحد:

$e = \ lim_ {x \ rightarrow 0} \ left (1+ \ right x) ^ \ frac {1} {x}$

يتم تعريف ثابت e على أنه سلسلة لانهائية:

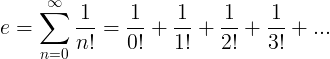
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ frac {1} {3!} + ...$

خصائص البريد

متبادل من e

مقلوب e هو الحد:

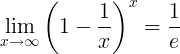
$\ lim_ {x \ rightarrow \ infty} \ left (1- \ frac {1} {x} \ right) ^ x = \ frac {1} {e}$

مشتقات ه

مشتق الدالة الأسية هو الدالة الأسية:

( ه ^س ) '= ه ^س

مشتق دالة اللوغاريتم الطبيعي هو دالة متبادلة:

(تسجيل _البريد x ) '= (ln x )' = 1 / x

تكاملات e

التكامل غير المحدود للدالة الأسية e ^x هو الدالة الأسية e ^x .

∫ e ^x dx = e ^x + c

التكامل غير المحدد لوظيفة اللوغاريتم الطبيعي log _e x هو:

∫ السجل _e x dx = ∫ ln x dx = x ln x - x + c

التكامل المحدد من 1 إلى e للدالة المتبادلة 1 / x هو 1:

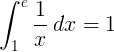
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

قاعدة e اللوغاريتم

يُعرَّف اللوغاريتم الطبيعي للرقم x على أنه اللوغاريتم الأساسي e لـ x:

قانون الجنسية س = سجل _ه س

دالة أسية

يتم تعريف الوظيفة الأسية على النحو التالي:

و ( س ) = إكسب ( س ) = ه ^س

صيغة أويلر

الرقم المركب e ^iθ له الهوية:

البريد ^iθ = cos ( θ ) + أنا الخطيئة ( θ )

i هي الوحدة التخيلية (الجذر التربيعي للعدد -1).

θ هو أي رقم حقيقي.