قواعد الأس

قواعد الأس وقوانين الأس والأمثلة.

ما هو الأس

القاعدة a المرفوعة للقوة n تساوي ضرب a ، n مرة:

أ ن = أ × أ × ... × أ

                    مرات n

a هو الأساس و n هو الأس.

أمثلة

3 1 = 3

3 2 = 3 × 3 = 9

3 3 = 3 × 3 × 3 = 27

3 4 = 3 × 3 × 3 × 3 = 81

3 5 = 3 × 3 × 3 × 3 × 3 = 243

قواعد وخصائص الدعاة

اسم القاعدة قاعدة مثال
قواعد المنتج أ ن ⋅ أ م = أ ن + م 2 3 ⋅ 2 4 = 2 3 + 4 = 128
أ ن ⋅ ب ن = ( أ ⋅ ب ) ن 3 2 ⋅ 4 2 = (3⋅4) 2 = 144
قواعد الحاصل أ ن / أ م = أ ن - م 2 5 /2 3 = 2 5-3 = 4
أ ن / ب ن = ( أ / ب ) ن 4 3 /2 3 = (4/2) 3 = 8
قواعد القوة ( ب ن ) م = ب n⋅m (2 3 ) 2 = 2 3⋅2 = 64
ب ن م = ب ( ن م ) 2 3 2 = 2 ( 3 2 ) = 512
م √ ( ب ن ) = ب ن / م 2 √ ( 6 2 ) = 2 6/2 = 8
ب 1 / ن = ن √ ب 8 1/3 = 3 √ 8 = 2
الأس السالب ب -n = 1 / ب ن 2 -3 = 1/2 3 = 0.125
قواعد الصفر ب 0 = 1 5 0 = 1
0 n = 0 ، لـ n / 0 0 5 = 0
قواعد واحدة ب 1 = ب 5 1 = 5
1 ن = 1 1 5 = 1
ناقص قاعدة واحدة 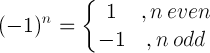(-1) 5 = -1
القاعدة المشتقة ( س ن ) ' = ن ⋅ س ن -1 ( × 3 ) ' = 3⋅ × 3-1
حكم لا يتجزأ ∫ س ن DX = س ن +1 / ( ن +1) + C ∫ x 2 dx = x 2 + 1 / (2 + 1) + C

قواعد منتج الدعاة

حكم المنتج مع نفس القاعدة

أ ن ⋅ أ م = أ ن + م

مثال:

2 3 ⋅ 2 4 = 2 3 + 4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅22 = 128

قاعدة المنتج مع نفس الأس

أ ن ⋅ ب ن = ( أ ⋅ ب ) ن

مثال:

3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 12⋅12 = 144

انظر: ضرب الأسس

قواعد حاصل الأس

قاعدة حاصل القسمة مع نفس القاعدة

أ ن / أ م = أ ن - م

مثال:

2 5 /2 3 = 2 5-3 = 2 2 = 4 = 2⋅2

قاعدة حاصل القسمة مع نفس الأس

أ ن / ب ن = ( أ / ب ) ن

مثال:

4 3 /2 3 = (4/2) 3 = 2 3 = 2⋅2⋅2 = 8

انظر: قسمة الأسس

قواعد قوة الدعاة

حكم القوة أنا

( و ن ) م = و n⋅m

مثال:

(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64

حكم القوة II

أ ن م = أ ( ن م )

مثال:

2 3 2 = 2 (3 2 ) = 2 (3⋅3) = 9 2 = 2⋅2⋅2⋅2⋅2⋅2⋅22 = 512

حكم القوة مع الراديكاليين

م √ ( أ ن ) = أ ن / م

مثال:

2 √ ( 6 2 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8

قاعدة الأس السالب

ب -n = 1 / ب ن

مثال:

2 -3 = 1/2 3 = 1 / (2⋅2⋅2) = 1/8 = 0.125

انظر: الأسس السلبية

 

آلة حاسبة الأس

 

أنظر أيضا

أعداد
جداول سريعة