আরকসিন ফাংশন
আরকসিন (এক্স), পাপ -১ (এক্স), বিপরীত সাইন ফাংশন।
আরকসিন সংজ্ঞা
X এর আরকসাইন x -1≤x≤1 যখন এক্স এর বিপরীত সাইন ফাংশন হিসাবে সংজ্ঞায়িত করা হয় ।
যখন y এর সাইন x এর সমান হবে:
sin y = x
তারপরে x এর আরকসিনটি x এর বিপরীত সাইন ফাংশনের সমান, যা y এর সমান:
আরকসিন x = পাপ -1 x = y
উদাহরণ
আরকসিন 1 = পাপ -1 1 = π / 2 রেড = 90 ° °
আরকসিনের গ্রাফ
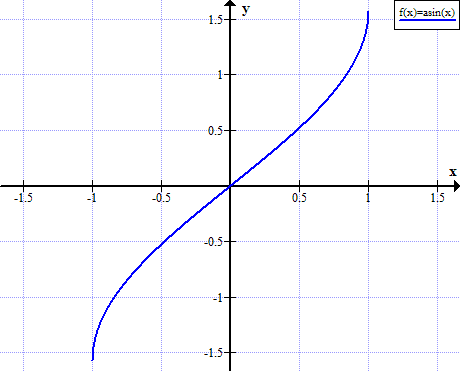
আরকসিন বিধি
| বিধি নাম | নিয়ম |
|---|---|
| আরকসিনের সাইন | sin (আরকসিন এক্স ) = এক্স |
| সাইন এর আরসাইন | arcsin (পাপ এক্স ) = x এর +2 ট π, যখন ট ∈ℤ ( ট পূর্ণসংখ্যা) |
| নেতিবাচক যুক্তির আরকসিন | আরকসিন (- x ) = - আরকসিন এক্স |
| পরিপূরক কোণ | আরকসিন x = π / 2 - আরসিকোস x = 90 ° - আরসিকোস এক্স |
| আরকসিন যোগফল | আরকসিন α + আরকসিন ( β ) = আরকসিন ( α√ (1- β 2 ) + β√ (1- α 2 ) ) |
| আরকসিন পার্থক্য | আরকসিন α - আরকসিন ( β ) = আরকসিন ( α√ (1- β 2 ) - β√ (1- α 2 ) ) |
| আরকসিনের কোসিন | |
| আরকসিনের স্পর্শকাতর | |
| আরকসিনের ডেরাইভেটিভ | 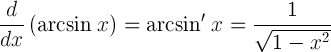 |
| আরকসিনের অনির্দিষ্ট অবিচ্ছেদ্য |
আরকসিন টেবিল
| এক্স | আরকসিন (এক্স) (রেড) |
আরকসিন (এক্স) (°) |
|---|---|---|
| -1 | -π / 2 | -90 ° |
| -√ 3 /2 | -π / 3 | -60 ° |
| -√ 2 /2 | -π / 4 | -45 ° |
| -১/২ | -π / 6 | -30 ° |
| 0 | 0 | 0 |
| ১/২ | π / 6 | 30 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 3 | 60 ° |
| 1 | π / 2 | 90 ° |
আরো দেখুন
- সাইন ফাংশন
- আরকোসিন ফাংশন
- আর্টিকান ফাংশন
- আরকসিন ক্যালকুলেটর
- রেডিয়ান রূপান্তরকারী ডিগ্রি
- আরকারসিন ০
- আরকসিনের ঘ
- অনন্তের আরকসিন
- আরকসিন গ্রাফ
- আরকসিন ডেরাইভেটিভ
- আরকসিন অবিচ্ছেদ্য
- আরকসিনের পাপ
- আর্কসিন কস
- আরকসিনের ট্যান