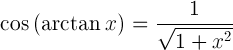আর্টাক্যানজেন্ট ফাংশন
আর্টিকান (এক্স), ট্যান -1 (এক্স), বিপরীতমুখী স্পর্শক কার্য।
আর্টিকান সংজ্ঞা
X এর আর্কট্যানজেন্টকে x এর বিপরীত স্পর্শক ফাংশন হিসাবে সংজ্ঞায়িত করা হয় যখন x আসল (x ∈ℝ ) হয়।
যখন y এর স্পর্শকটি x এর সমান হয়:
ট্যান y = এক্স
তারপরে x এর আর্কট্যানজেন্টটি x এর বিপরীতমুখী কার্যের সমান, যা y এর সমান:
আর্টিকান x = ট্যান -1 x = y
উদাহরণ
আর্টকান 1 = ট্যান -1 1 = π / 4 রেড = 45 ° °
আর্টিকানের গ্রাফ
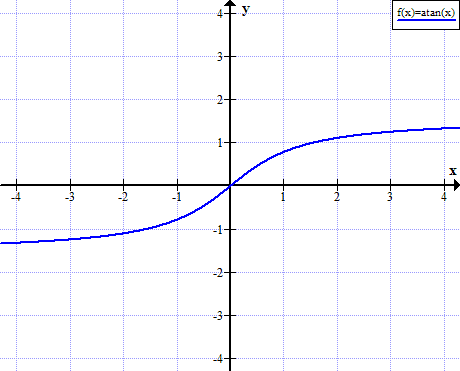
আর্টিকান বিধি
| বিধি নাম | নিয়ম |
|---|---|
| আর্টাক্যানজেন্টের স্পর্শকাতর | ট্যান (আর্টিকান এক্স ) = এক্স |
| নেতিবাচক যুক্তির আর্টিকান | আর্টিকান (- x ) = - আর্টিকান এক্স |
| আর্টিকান যোগফল | আর্টিকান α + আর্টকান β = আর্টিকান [( α + β ) / (1- αβ )] |
| আর্টিকান পার্থক্য | আর্টিকান α - আর্টিকান β = আর্টিকান [( α - β ) / (1+ αβ )] |
| আর্টাক্যানজেন্ট এর সাইন | |
| আর্টাক্যানজেন্টের কোসিন | |
| পারস্পরিক যুক্তি | 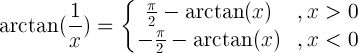 |
| আর্টসিন থেকে আর্টিকান | |
| আর্টিকান এর ডেরাইভেটিভ | |
| আর্টিকানের অনির্দিষ্ট অবিচ্ছেদ্য | |
আর্টিকান টেবিল
| এক্স | আর্টিকান (এক্স) (রেড) |
আর্টিকান (এক্স) (°) |
|---|---|---|
| -∞ | -π / 2 | -90 ° |
| -৩ | -1.2490 | -71.565 ° |
| -২ | -1.1071 | -63.435 ° |
| -√ 3 | -π / 3 | -60 ° |
| -1 | -π / 4 | -45 ° |
| -1 / √ 3 | -π / 6 | -30 ° |
| -0.5 | -0.4636 | -26.565 ° |
| 0 | 0 | 0 |
| 0.5 | 0.4636 | 26.565 ° |
| 1 / √ 3 | π / 6 | 30 ° |
| 1 | π / 4 | 45 ° |
| । 3 | π / 3 | 60 ° |
| 2 | 1.1071 | 63.435 ° |
| 3 | 1.2490 | 71.565 ° |
| ∞ | π / 2 | 90 ° |
আরো দেখুন
- স্পর্শকাতর কাজ
- আরকোসিন ফাংশন
- আরকসিন ফাংশন
- আর্টিকান 0
- আর্টিকান।
- আর্টিকান 2
- অনন্তের আর্টিকান
- আর্টিকান এর ডেরাইভেটিভ
- আর্টিকানের ইন্টিগ্রাল
- আর্টিকান সাইন
- আর্টিকানের কোসিন
- আর্টিকান গ্রাফ
- আর্টকান ক্যালকুলেটর
- রেডিয়ান রূপান্তরকারী ডিগ্রি
ট্রিগনোমেট্রি
দ্রুত টেবিল