Arcsine funktion
bueform (x), sin -1 (x), invers sinusfunktion .
Definition af Arcsin
Bueskinnen på x defineres som den inverse sinusfunktion på x, når -1≤x≤1.
Når sinus på y er lig med x:
sin y = x
Derefter er buen af x lig med den inverse sinusfunktion af x, som er lig med y:
bueform x = sin -1 x = y
Eksempel
bueform 1 = sin -1 1 = π / 2 rad = 90 °
Graf af bueskind
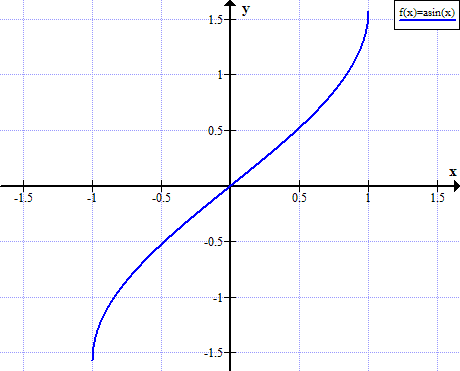
Arcsin regler
| Regelnavn | Herske |
|---|---|
| Sinus af buesine | sin (bueform x ) = x |
| Bue af sinus | bueform (sin x ) = x +2 k π, når k ∈ℤ ( k er heltal) |
| Arcsin af negativt argument | bueform (- x ) = - bueform x |
| Supplerende vinkler | bueform x = π / 2 - arccos x = 90 ° - arccos x |
| Arcsin sum | buesin α + buesin ( β ) = buesin ( α√ (1- β 2 ) + β√ (1- α 2 ) ) |
| Arcsin forskel | buesin α - buesin ( β ) = buesin ( α√ (1- β 2 ) - β√ (1- α 2 ) ) |
| Kosinus af bueskind | |
| Tangent af buesine | |
| Afledt af buesine | 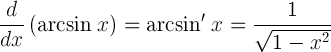 |
| Ubestemt integral af buesine |
Arcsin bord
| x | bueform (x) (rad) |
bueform (x) (°) |
|---|---|---|
| -1 | -π / 2 | -90 ° |
| -√ 3 /2 | -π / 3 | -60 ° |
| -√ 2 /2 | -π / 4 | -45 ° |
| -1/2 | -π / 6 | -30 ° |
| 0 | 0 | 0 ° |
| 1/2 | π / 6 | 30 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 3 | 60 ° |
| 1 | π / 2 | 90 ° |
Se også
- Sinus funktion
- Arccosine funktion
- Arctan-funktion
- Arcsin-lommeregner
- Grad til radianomformer
- Bueskinne på 0
- Bueskinne på 1
- Uendelig bue
- Arcsin-graf
- Arcsin-derivat
- Arcsin integreret
- Synd af bueskind
- Cos af bueskind
- Tan af bueskind