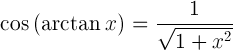Arktangensfunktion

Arctan (x), tan ^-1 (x), inverse Tangentenfunktion .

• Definition von Arctan
• Grafik von Arctan
• Arktanische Regeln
• Arctan Tisch
• Arctan Rechner

Arktanische Definition

Der Arkustangens von x ist definiert als die inverse Tangentenfunktion von x, wenn x real ist (x ∈ℝ ).

Wenn die Tangente von y gleich x ist:

tan y = x

Dann ist der Arkustangens von x gleich der inversen Tangentenfunktion von x, die gleich y ist:

Arctan x = tan ^-1 x = y

Beispiel

Arctan 1 = tan ^-1 1 = π / 4 rad = 45 °

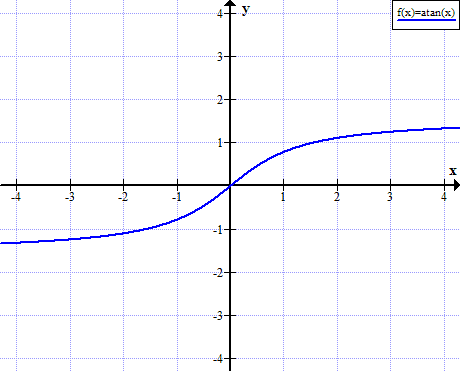
Grafik von Arctan

Arktanische Regeln

Regelname	Regel
Tangente des Arkustangens	tan (arctan x ) = x
Arctan des negativen Arguments	Arctan (- x ) = - Arctan x
Arktanische Summe	Arctan α + Arctan β = Arctan [( α + β ) / (1- αβ )]
Arctan Unterschied	Arctan α - Arctan β = Arctan [( α - β ) / (1+ αβ )]
Sinus des Arkustangens
Kosinus des Arkustangens
Gegenseitiges Argument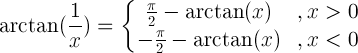
Arctan aus Arcsin
Derivat von Arctan
Unbestimmtes Integral von Arctan

Arctan Tisch

x	Arctan (x) (rad)	Arctan (x) (°)
-∞	-π / 2	-90 °
-3	-1,2490	-71,565 °
-2	-1.1071	-63,435 °
-√ 3	-π / 3	-60 °
-1	-π / 4	-45 °
-1 / √ 3	-π / 6	-30 °
-0,5	-0,4636	-26,565 °
0	0	0 °
0,5	0,4636	26,565 °
1 / √ 3	π / 6	30 °
1	π / 4	45 °
√ 3	π / 3	60 °
2	1.1071	63,435 °
3	1,2490	71,565 °
∞	π / 2	90 °

 

 

---

Siehe auch

• Tangentenfunktion
• Arccosin-Funktion
• Arcsine-Funktion
• Arctan von 0
• Arctan von 1
• Arctan von 2
• Arctan der Unendlichkeit
• Derivat von Arctan
• Integral von Arctan
• Sinus von Arctan
• Kosinus von Arctan
• Arktan Graph
• Arctan Rechner
• Konverter von Grad zu Bogenmaß