Arcsine-Funktion
Arcsin (x), sin -1 (x), inverse Sinusfunktion .
Arcsin-Definition
Der Arkussinus von x ist definiert als die inverse Sinusfunktion von x, wenn -1 ≤ x ≤ 1 ist.
Wenn der Sinus von y gleich x ist:
sin y = x
Dann ist der Arkussinus von x gleich der inversen Sinusfunktion von x, die gleich y ist:
arcsin x = sin -1 x = y
Beispiel
arcsin 1 = sin -1 1 = π / 2 rad = 90 °
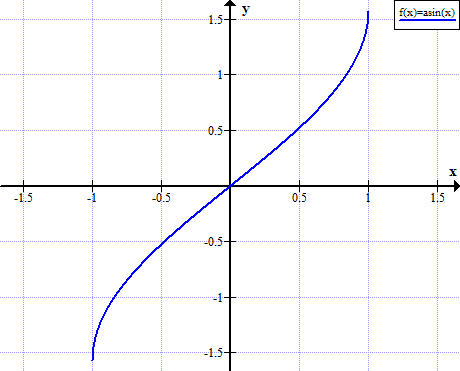
Graph von Arcsin
Arcsin-Regeln
| Regelname | Regel |
|---|---|
| Sinus von Arkusinus | sin (arcsin x ) = x |
| Sinus Arcus | arcsin (sin x ) = x +2 k π, wenn k ∈ℤ ( k ist eine ganze Zahl) |
| Arcsin des negativen Arguments | arcsin (- x ) = - arcsin x |
| Komplementäre Winkel | arcsin x = π / 2 - arccos x = 90 ° - arccos x |
| Arcsin Summe | Arcsin α + Arcsin ( β ) = Arcsin ( α√ (1- β 2 ) + β√ (1- α 2 ) ) |
| Arcsin Unterschied | Arcsin α - Arcsin ( β ) = Arcsin ( α√ (1- β 2 ) - β√ (1- α 2 ) ) |
| Kosinus von Arkusinus | |
| Tangens von Arkussinus | |
| Ableitung von Arkussinus | 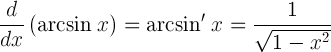 |
| Unbestimmtes Integral des Arkussinus |
Arcsin Tisch
| x | Arcsin (x) (rad) |
Arcsin (x) (°) |
|---|---|---|
| -1 | -π / 2 | -90 ° |
| -√ 3 /2 | -π / 3 | -60 ° |
| -√ 2 /2 | -π / 4 | -45 ° |
| -1/2 | -π / 6 | -30 ° |
| 0 | 0 | 0 ° |
| 1/2 | π / 6 | 30 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 3 | 60 ° |
| 1 | π / 2 | 90 ° |
Siehe auch
- Sinusfunktion
- Arccosin-Funktion
- Arktanfunktion
- Arcsin-Rechner
- Konverter von Grad zu Bogenmaß
- Arcsin von 0
- Arcsin von 1
- Arcsin der Unendlichkeit
- Arcsin-Diagramm
- Arcsin-Derivat
- Arcsin Integral
- Sünde von Arcsin
- Cos von Arcsin
- Tan von Arcsin