ε σταθερά

Η σταθερά ή ο αριθμός του Euler είναι μια μαθηματική σταθερά. Η σταθερά e είναι πραγματικός και παράλογος αριθμός.

ε = 2.718281828459 ...

Ορισμός του e
Ιδιότητες του e
Βάση και λογάριθμος
Εκθετικη συναρτηση
Η φόρμουλα του Euler

Ορισμός του e

Η σταθερά e ορίζεται ως το όριο:

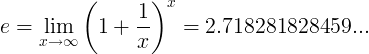
$e = \ lim_ {x \ rightarrow \ infty} \ αριστερά (1+ \ frac {1} {x} \ δεξιά) ^ x = 2.718281828459 ...$

Εναλλακτικοί ορισμοί

Η σταθερά e ορίζεται ως το όριο:

$e = \ lim_ {x \ rightarrow 0} \ αριστερά (1+ \ δεξιά x) ^ \ frac {1} {x}$

Η σταθερά e ορίζεται ως η άπειρη σειρά:

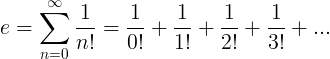
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ Frac {1} {3!} + ...$

Ιδιότητες του e

Αμοιβαία του e

Το αντίστροφο του e είναι το όριο:

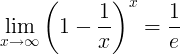
$\ lim_ {x \ rightarrow \ infty} \ αριστερά (1- \ frac {1} {x} \ δεξιά) ^ x = \ frac {1} {e}$

Παράγωγα του e

Το παράγωγο της εκθετικής συνάρτησης είναι η εκθετική συνάρτηση:

( e ^x ) '= e ^x

Το παράγωγο της συνάρτησης φυσικού λογάριθμου είναι η αμοιβαία συνάρτηση:

(log _e x ) '= (ln x )' = 1 / x

Ολοκληρώματα του e

Η αόριστη ολοκλήρωση της εκθετικής συνάρτησης e ^x είναι η εκθετική συνάρτηση e ^x .

∫ e ^x dx = e ^x + c

Η αόριστη ολοκλήρωση της συνάρτησης φυσικού λογάριθμου log _e x είναι:

∫ log _e x dx = ∫ ln x dx = x ln x - x + c

Το οριστικό ακέραιο από 1 έως e της αμοιβαίας συνάρτησης 1 / x είναι 1:

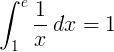
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

Βάση και λογάριθμος

Ο φυσικός λογάριθμος ενός αριθμού x ορίζεται ως ο βασικός λογάριθμος του x:

ln x = καταγραφή _e x

Εκθετικη συναρτηση

Η εκθετική συνάρτηση ορίζεται ως:

f ( x ) = exp ( x ) = e ^x

Η φόρμουλα του Euler

Ο σύνθετος αριθμός e ^iθ έχει την ταυτότητα:

e ^iθ = cos ( θ ) + i sin ( θ )

είμαι η φανταστική μονάδα (η τετραγωνική ρίζα του -1).

θ είναι οποιοσδήποτε πραγματικός αριθμός.