Μηδενικός αριθμός (0)
- Ορισμός μηδενικού αριθμού
- Μηδέν ιστορικό αριθμών
- Μηδενικές ιδιότητες αριθμού
- Σετ που περιέχουν μηδέν
Ορισμός μηδενικού αριθμού
Το μηδέν είναι ένας αριθμός που χρησιμοποιείται στα μαθηματικά για να περιγράψει καμία ποσότητα ή μηδενική ποσότητα.
Όταν υπάρχουν 2 μήλα στο τραπέζι και πάρουμε τα 2 μήλα, μπορούμε να πούμε ότι δεν υπάρχουν μήλα στο τραπέζι.
Ο μηδενικός αριθμός δεν είναι θετικός και όχι αρνητικός αριθμός.
Το μηδέν είναι επίσης ένα ψηφίο κράτησης θέσης σε άλλους αριθμούς (π.χ. 40,103, 170).
Είναι μηδέν αριθμός;
Το μηδέν είναι ένας αριθμός. Δεν είναι θετικός ούτε αρνητικός αριθμός.
Μηδέν ψηφίο
Το μηδέν ψηφίο χρησιμοποιείται ως σύμβολο κράτησης θέσης κατά τη σύνταξη αριθμών.
Για παράδειγμα:
204 = 2 × 100 + 0 × 10 + 4 × 1
Μηδέν ιστορικό αριθμών
Ποιος εφηύρε τον μηδέν αριθμό;
Το σύγχρονο σύμβολο 0 εφευρέθηκε στην Ινδία τον 6ο αιώνα, που χρησιμοποιήθηκε αργότερα από τους Πέρσες και τους Άραβες και αργότερα στην Ευρώπη.
Σύμβολο του μηδέν
Ο μηδενικός αριθμός συμβολίζεται με το σύμβολο 0 .
Το αραβικό αριθμητικό σύστημα χρησιμοποιεί το σύμβολο ٠.
Μηδενικές ιδιότητες αριθμού
x αντιπροσωπεύει οποιονδήποτε αριθμό.
| Λειτουργία | Κανόνας | Παράδειγμα |
|---|---|---|
Πρόσθεση |
x + 0 = x |
3 + 0 = 3 |
Αφαίρεση |
x - 0 = x |
3 - 0 = 3 |
Πολλαπλασιασμός |
x × 0 = 0 |
5 × 0 = 0 |
Διαίρεση |
0 ÷ x = 0 , όταν x ≠ 0 |
0 ÷ 5 = 0 |
| Το x ÷ 0 είναι απροσδιόριστο |
Το 5 ÷ 0 είναι απροσδιόριστο |
|
Εκτόνωση |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Ρίζα |
√ 0 = 0 |
|
Λογάριθμος |
Το log b (0) είναι απροσδιόριστο |
|
| |
||
Παραγοντικό |
0! = 1 |
|
Ημίτονο |
sin 0º = 0 |
|
Συνημίτονο |
cos 0º = 1 |
|
Εφαπτομένος |
μαύρισμα 0º = 0 |
|
Παράγωγο |
0 '= 0 |
|
Αναπόσπαστο |
∫ 0 d x = 0 + C |
|
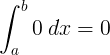 |
Μηδενική προσθήκη
Η προσθήκη ενός αριθμού συν μηδέν ισούται με τον αριθμό:
x + 0 = x
Για παράδειγμα:
5 + 0 = 5
Μηδενική αφαίρεση
Η αφαίρεση ενός αριθμού μείον μηδέν ισούται με τον αριθμό:
x - 0 = x
Για παράδειγμα:
5 - 0 = 5
Πολλαπλασιασμός με μηδέν
Ο πολλαπλασιασμός ενός αριθμού φορές μηδέν ισούται με μηδέν:
x × 0 = 0
Για παράδειγμα:
5 × 0 = 0
Ο αριθμός διαιρείται με μηδέν
Η διαίρεση ενός αριθμού με μηδέν δεν ορίζεται:
Το x ÷ 0 είναι απροσδιόριστο
Για παράδειγμα:
Το 5 ÷ 0 είναι απροσδιόριστο
Μηδέν διαιρούμενο με έναν αριθμό
Η διαίρεση ενός μηδέν με έναν αριθμό είναι μηδέν:
0 ÷ x = 0
Για παράδειγμα:
0 ÷ 5 = 0
Αριθμός έως τη μηδενική ισχύ
Η ισχύς ενός αριθμού που αυξάνεται με μηδέν είναι μία:
x 0 = 1
Για παράδειγμα:
5 0 = 1
Λογόριθμος μηδέν
Ο λογάριθμος βάσης b του μηδέν δεν είναι καθορισμένος:
Το log b (0) είναι απροσδιόριστο
Δεν υπάρχει αριθμός που μπορούμε να ανεβάσουμε τη βάση b για να πάρουμε μηδέν.
Μόνο το όριο του λογαρίθμου βάσης b του x, όταν το x συγκλίνει μηδέν είναι μείον άπειρο:
![]()
Σετ που περιέχουν μηδέν
Το μηδέν είναι ένα στοιχείο των φυσικών αριθμών, ακέραιων αριθμών, πραγματικών αριθμών και σύνθετων αριθμών:
| Σετ | Ορισμός συμβολής ιδιότητας μέλους |
|---|---|
| Φυσικοί αριθμοί (μη αρνητικοί) | 0 ∈ ℕ 0 |
| Ακέραιοι αριθμοί | 0 ∈ ℤ |
| Πραγματικοί αριθμοί | 0 ∈ ℝ |
| Σύνθετοι αριθμοί | 0 ∈ ℂ |
| Ρητοί αριθμοί | 0 ∈ ℚ |
Είναι μηδέν ή μονός αριθμός;
Το σύνολο των ζυγών αριθμών είναι:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Το σύνολο των μονών αριθμών είναι:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Το μηδέν είναι ένα ακέραιο πολλαπλάσιο των 2:
0 × 2 = 0
Το Zero είναι μέλος του συνόλου των ζυγών αριθμών:
0 ∈ {2 k , k ∈ℤ}
Έτσι, το μηδέν είναι ένας ζυγός αριθμός και όχι ένας μονός αριθμός.
Είναι μηδέν ένας φυσικός αριθμός;
Υπάρχουν δύο ορισμοί για το σύνολο φυσικών αριθμών.
Το σύνολο των μη αρνητικών ακέραιων αριθμών:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Το σύνολο των θετικών ακεραίων:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Το Zero είναι μέλος του συνόλου μη αρνητικών ακέραιων αριθμών:
0 ∈ ℕ 0
Το Zero δεν είναι μέλος του συνόλου θετικών ακεραίων:
0 ∉ ℕ 1
Είναι μηδέν ακέραιος αριθμός;
Υπάρχουν τρεις ορισμοί για ολόκληρους αριθμούς:
Το σύνολο ακέραιων αριθμών:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Το σύνολο των μη αρνητικών ακέραιων αριθμών:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Το σύνολο των θετικών ακεραίων:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Το μηδέν είναι μέλος του συνόλου ακέραιων αριθμών και του συνόλου μη αρνητικών ακέραιων αριθμών:
0 ∈ ℤ
0 ∈ ℕ 0
Το Zero δεν είναι μέλος του συνόλου θετικών ακεραίων:
0 ∉ ℕ 1
Το μηδέν είναι ακέραιος αριθμός;
Το σύνολο ακέραιων αριθμών:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Το μηδέν είναι μέλος του συνόλου ακέραιων αριθμών:
0 ∈ ℤ
Έτσι το μηδέν είναι ακέραιος αριθμός.
Είναι μηδέν ένας λογικός αριθμός;
Ο λογικός αριθμός είναι ένας αριθμός που μπορεί να εκφραστεί ως πηλίκο δύο ακέραιων αριθμών:
ℚ = { n / m ; ν , μ ∈ℤ}
Το μηδέν μπορεί να γραφτεί ως πηλίκο δύο ακέραιων αριθμών.
Για παράδειγμα:
0 = 0/3
Έτσι το μηδέν είναι λογικός αριθμός.
Είναι μηδέν θετικός αριθμός;
Ο θετικός αριθμός ορίζεται ως αριθμός μεγαλύτερος από το μηδέν:
x / 0
Για παράδειγμα:
5/ 0
Δεδομένου ότι το μηδέν δεν είναι μεγαλύτερο από το μηδέν, δεν είναι θετικός αριθμός.
Είναι μηδέν ένας πρωταρχικός αριθμός;
Ο αριθμός 0 δεν είναι πρωταρχικός αριθμός.
Το μηδέν δεν είναι θετικός αριθμός και έχει άπειρο αριθμό διαιρετών.
Ο χαμηλότερος πρώτος αριθμός είναι 2.