e konstantne
Konstant ehk Euleri arv on matemaatiline konstant. E konstant on tegelik ja irratsionaalne arv.
e = 2,718281828459 ...
Mõiste e
E konstant on määratletud kui piir:
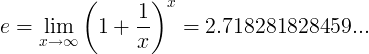
Alternatiivsed määratlused
E konstant on määratletud kui piir:
![]()
E konstant on määratletud kui lõpmatu jada:
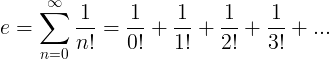
E. Omadused
Vastastikune e
E vastastikune väärtus on piir:
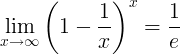
Tuletised e
Eksponentsiaalfunktsiooni tuletis on eksponentsiaalfunktsioon:
( e x ) '= e x
Loodusliku logaritmi funktsiooni tuletis on vastastikune funktsioon:
(log e x ) '= (ln x )' = 1 / x
Integraalid e
Umbmäärases integraali eksponentfunktsiooni e x on eksponentfunktsiooni e x .
∫ e x dx = e x + c
Loodusliku logaritmi funktsiooni log e x määramatu integraal on:
∫ log e x dx = ∫ ln x dx = x ln x - x + c
Vastastikuse funktsiooni 1 / x kindel integraal vahemikus 1 kuni e on 1:
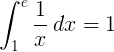
Baas e logaritm
Arvu x loomulik logaritm on määratletud kui x-i põhilogaritm:
ln x = log e x
Eksponentsiaalne funktsioon
Eksponentsiaalfunktsioon on määratletud järgmiselt:
f ( x ) = exp ( x ) = e x
Euleri valem
Kompleksarvul e iθ on identiteet:
e iθ = cos ( θ ) + i patt ( θ )
i on kujuteldav üksus (ruutjuur -1).
θ on mis tahes tegelik arv.
Vaata ka
- Kuidas e on 2,71828183?
- Logaritmireeglid
- Looduslik logaritm
- Eksponentide reeglid
- Normaalne jaotus
- Pi konstant
- e konstant - vikipeedia