e vakio

Vakio tai Eulerin luku on matemaattinen vakio. E-vakio on todellinen ja irrationaaliluku.

e = 2,718281828459 ...

Määritelmä e
E. Ominaisuudet
Perus e-logaritmi
Eksponentti funktio
Eulerin kaava

Määritelmä e

E-vakio määritellään rajaksi:

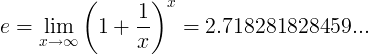
$e = \ lim_ {x \ rightarrow \ infty} \ vasen (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...$

Vaihtoehtoiset määritelmät

E-vakio määritellään rajaksi:

$e = \ lim_ {x \ oikeanpuoleinen 0} \ vasen (1+ \ oikea x) ^ \ frac {1} {x}$

E-vakio määritellään loputtomaksi sarjaksi:

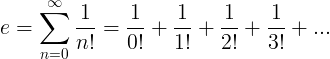
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ Frac {1} {3!} + ...$

E. Ominaisuudet

Vastavuoroinen e

E: n vastavuoroisuus on raja:

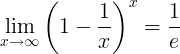
$\ lim_ {x \ rightarrow \ infty} \ vasen (1- \ frac {1} {x} \ right) ^ x = \ frac {1} {e}$

Johdannaiset e

Eksponenttifunktion derivaatti on eksponenttifunktio:

( e ^x ) '= e ^x

Luonnollisen logaritmifunktion derivaatti on vastavuoroinen funktio:

(log _e x ) '= (ln x )' = 1 / x

E. Integraalit

Määräämättömäksi ajaksi integraali eksponenttifunktio e ^x on eksponentiaalinen funktio e ^x .

∫ e ^x dx = e ^x + c

Luonnollisen logaritmin funktion log _e x määrittelemätön integraali on:

∫ log _e x dx = ∫ ln x dx = x ln x - x + c

Vastavuoroisen funktion 1 / x lopullinen integraali välillä 1 - e on 1:

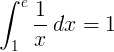
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

Perus e-logaritmi

Luvun x luonnollinen logaritmi määritellään x: n perus e-logaritmiksi:

ln x = log _e x

Eksponentti funktio

Eksponenttifunktio määritellään seuraavasti:

f ( x ) = exp ( x ) = e ^x

Eulerin kaava

Kompleksiluvulla e ^iθ on identiteetti:

e ^iθ = cos ( θ ) + i sin ( θ )

i on kuvitteellinen yksikkö (neliöjuuri -1).

θ on mikä tahansa reaaliluku.